
英语原文共 27 页,剩余内容已隐藏,支付完成后下载完整资料
16.1 背景
在前面的章节里,我们已经讨论过建立多元时间序列的数据生成过程中的条件均值,条件为过去每一个特殊时点。在那样的环境中,条件分布的方差和协方差矩阵是被假设为时不变的。事实上,在这些讨论中,残差或预测误差是被假定为独立白噪声的。这样的简化在许多应用中是有用且合适的。
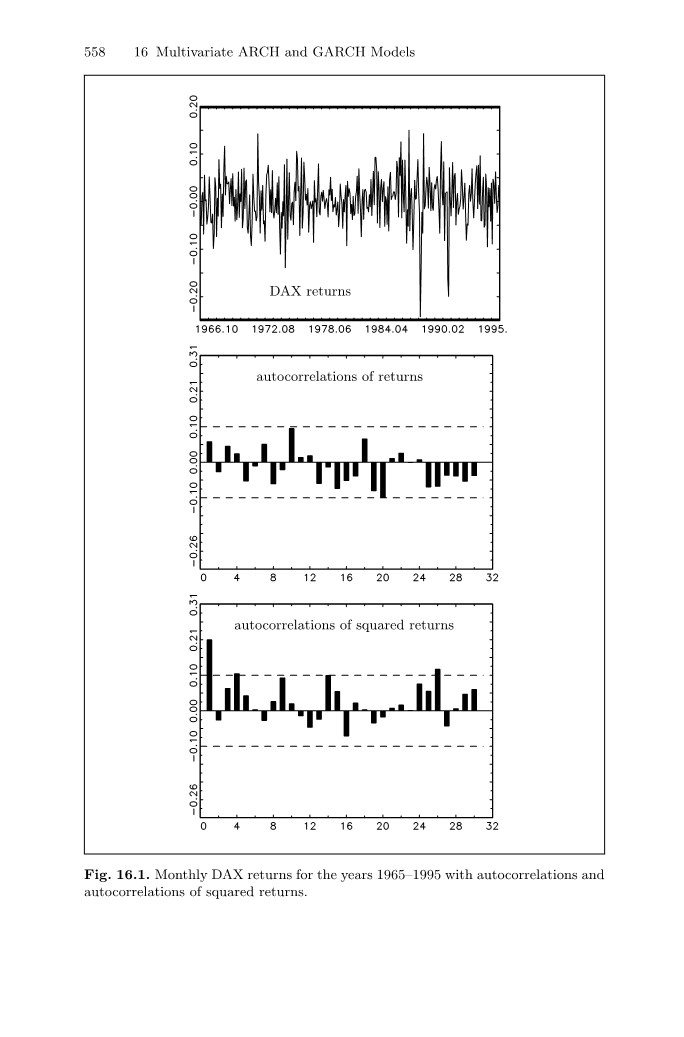
然而,也有一些情况,这样的假设是有问题的,例如,当分析金融时间序列时。来看这个例子,在1965-1995年间DAX(德国蓝筹股指数)的月收益,如图16.1。自相关系数全部都落在的带宽中,因此,根据第四章,第4.4节的讨论结果,一些人可能会总结为该月收益不是自相关的。如果他们不但是不相关的,而且是独立的,那么他们的平方值也是独立的。在这个例子中可以清晰地看到,在图16.1的第三段中,给出的平方收益也是自相关的。总之,在这种情况下,观察到独立性的假定相当于在AR(0)模型中独立的残差,,是存在明显问题的。根据第四章,第4.4节的置信区间结论,我们用到独立性假设,收益不相关的结论是值得怀疑的。
在图16.1中呈现的DAX平方收益相关性暗示这是条件异方差性。加上一点想象,在图中还能够看到DAX收益随着时间轻易地改变。样本收益上半阶段低于下半阶段。在许多时间序列中都存在相似的特性,尤其在金融市场序列中,激发了个别模型条件异方差数据的发展。
这可能引起争论,条件均值是最佳预测,因此,从预测的角度来看,波动的改变不是很重要的。然而,这个位置忽略了预测误差方差,也就是说,在建立预测区间时,条件分布的方差是必要的。当基于调查的预测方差是很希望得到的,考虑到条件异方差是同等重要的。然后,例如在金融数据分析中,在考虑之中的序列未来波动经常是有趣的去评估与资产有关的风险。在那样的情况下,预测方差是一定有直接利害关系的。更进一步说,在一些特殊市场中,与投资有关的市场波动对市场参与者的期望可能有直接的影响。因此,这里有从第二时刻到第一时刻的反馈。因此,建立更详细的时间序列波动模型的重要性是一件自然发展的事情,也被Englersquo;s(1982)发明的ARCH(条件异方差自回归)模型推动发展。到现在为止,ARCH模型在改变条件波动上,代表一类很大范围的模型。更多的,这也有一些文献在多元性方面做拓展,这又是本章的中心话题。
因为许多序列有很强的相关性,我们可以明显地推测到,一个序列波动的增强可能也会影响另一个序列的波动。例如,这可能发生在不同货币改变利率的时候, 不同到期日的债券利率,或者明确的市场交割股票收益。因此,条件异方差的多元模型是有意义的。
下面,对单变量ARCH模型以及广义的ARCH模型(ARCH)的实例进行简单地复习,然后我们将对扩展的多变量模型进行讨论。本章的本节报告是源于Engle和 kroner(1995)的一篇文章。这也有许多回顾的文章涵盖了多变量ARCH和GARCH模型,例如: Bollerslev , Engleamp;Nelson(1994), Beraamp;Higgins(1993), Bauwens, Laurent amp; Bombouts(2004) , Bollerslev , Chou amp; Kroner(1992) , and Pagan(1996).后者的两篇文章也纵览了一些实用的文献。
16.2 单变量GARCH模型
16.2.1 定义
考虑到单变量连续不相关,零均值过程为。例如,可能代表自回归的残差。会随着条件异方差自回归过程ARCH(q),如果条件分布给定他的过去,含有零均值和条件方差:
(16.2.1)
即, 。另外,有时相当有用的方法去通过定义判别ARCH过程。
(16.2.2)
这里的假设比之前的仅仅有关前两个时刻的条件分布定义略微严格。下面,16.2.2的定义是有用的。通过这种方式生成的是零均值,连续不相关的。
最开始,Engle(1982)在他的ARCH模型原创论文中,假设条件分布是正态分布,因此,
(16.2.3)
虽然不同的分布在后面都会讨论,甚至这个特别的分布假设,但是模型能够通过与那些已有的观测数据相似的性质生成序列。特别的,它能够通过波动集聚性和异常值相似性生成序列,就像图16.1中DAX序列。即使基于ARCH(q)模型的条件分布是正态的,非条件分布则是非正态的。特别的,,叫做尖锋态分布,也就是说,他比正态分布有更多的尾部的值在0处波动,因此,它能够生成偶然的异常值。
然而,事实证明许多序列,即有着相当大的数据的ARCH过程在条件方差中捕获动态是必要的。因此,Bollerslev(1986)和Taylor(1986)建议,通过扩展模型获取更多的简约性,类比一个相似的行为,像AR模型扩展到ARMA模型。他们建议有着以下条件方差的广义的ARCH模型(GARCH):
(16.2.4)
这些模型被简单定义为GARCH(q,m)。他们通过存在的非条件方差生成数据,当且仅当参数的总和满足以下条件:
(16.2.5)
如果满足这个条件,有一个常数非条件方差,
(16.2.6)
GARCH和ARCH模型有关条件均值的相似之处是,定义:,将带入16.2.4式中,重新整合式子。我们可以得到
(16.2.7)
对而言,是一个正常的ARCH(q,m)模型。这里假设没有丢失一般性,即,并且有。
16.2.2 预测
虽然条件期望中,为0,因此,可选预测全部为0,当,这里是一个独立白噪声是一个重要的不同之处。如果是高斯过程,一个一步向前的预测区间有这样的结构形式:
这里表示预测值,通常,是与正态分布中有关的(参见2.2.3)。因此,预测区间是恒宽的,不管预测起始试点为多少。相反,如果是一个GARCH(q,m)过程,则修正的一步向前的预测区间为:
(16.2.8)
这里区间长度取决于这个过程的历史数据,因为条件标准差随时间变化。
为了证明这个现象,假设DAX收益调整后的均值是由GARCH(1,1)生成,条件主成分和条件方差为:
这个模型是的确适合1960-1991期间的Lutkepohl的月度DAX收益数据(1997)。 一步向前,95%预测区间见图16.2。此时,非条件方差为
假设错-数据是独立同分布的正态分布数据,利用之前的白噪声方差,导致恒定的预测区间,同样见图16.2。记录这些结果的暗示是重要的。置信区间完全忽略了波动中的方差,然而GARCH模型区间清楚地反应了在波动较大时,更多的预测不确定性,以及在股票市场波动较小时,更窄的区间。
就像之前提到的,如果残差是正态GARCH过程,观测数据的非条件分布将通常为非正态。
因此,在常态假设下,因为错误的分布假设,使得计算的预测置信区间可能并没有预期的95%的概率。非正态非条件分布的GARCH过程同样复杂化了多步区间预测。多步预测的公式和特性在Baillieamp;Bollerslev(1992)的论文中已经讨论过。没有详细的阐述,值得记录的是,在一个固定的过程中,当预测范围扩大,最佳的预测总是接近均值,伴随着非条件方差等于预测误差方差以及预测误差分布接近非条件分布,如果条件分布是正态的,那么这个过程大体是非正态的。
我们现在讨论如何扩展这些概念到向量过程的例子中区去。在那样的条件下,我们也将处理估计GARCH模型参数的问题。
16.3 多元GARCH模型
ARCH 和GARCH模型的多元扩展将会按照与VAR 和VARMA相似的规则去定义。早些关于多元ARCH 和GARCH模型的文章是由Engle,Granger amp;Kraft(1986),Diebold amp; Nerlove(1989),Bollerslev, Engle amp; Wooldridge(1988).在分析和估计这些模型中有许多复杂性,在这里我们将进行讨论。简单的多元ARCH模型将会先被讨论。
16.3.1 多元ARCH
假设是K维空间零均值连续不相关的过程,可能是一个动态的残差过程,可以用下式表示:
( 16.3.1)
这里是K维空间i.i.d的白噪声,,是关于的条件协方差矩阵,给定的,通常,是正定对称的,定义为的平方根。
(见索引A.9.2,关于正定矩阵平方根的详细解释)。很明显地,有一个条件分布,,有以下形式
(16.3.2)
他们代表多元ARCH(q)过程,如果满足以下条件:
(16.3.3)
这里,再一次表示半向量,从对角向下累加平方矩阵的列向量到一个向量,是维常数向量,是参数矩阵。不同的条件分布已经被假定并分析。例如,考虑一个多元正态条件分布,也就是说,,。虽然对于许多金融时间序列而言,这个分布可能不是最合适的,但是它能够起到一个作用,当参数估计已经在16.4节讨论过。代表金融时间序列的条件分布经常能更好地被更为肥尾的分布来代表,像有着低自由度的t分布。
例如,考虑一个二变量过程,
显然,甚至这样一个二向量序列简单模型都有相当一部分的参数,这使计算很难进行下去。特别的,这类型的一般模型关于方差和他们高阶矩的特征的关系是不明显的。因此,更严格的模型需要被建立。例如,Bollerslev等人在1988年发表的考虑对角ARCH过程,这里矩阵全是对角的。在第一个例子中,模型有如下形式:
即使这类模型的简单例子能够生成复杂的动态波动。此外,尽管他们的结构简单,过程却包含了不寻常的技术问题。其中的一个是参数必须是条件协方差矩阵全是正定的。为了证明这个特性,Baba,Engle,Kraftamp;Kroner(1990)以及Engleamp; Kroner(1995)研究以下多元ARCH模型的方差,
(16.3.4)
这里,是矩阵。这个特别的多变量模型已经被命名为BEKK模型。这里,是正定矩阵,如果有这样的特性,即通过将它写为乘积形式来被强制实施,,其中为三角矩阵。这个模型的另一个优势在于,它是相对简洁的。例如,对一个的二向量过程,这里仅有7个参数,而全模型有12个参数。更甚者,对比对角模型,它能够在条件二阶矩中产生相当多的交互作用。
16.3.2 MGARCH
大体上,多变量ARCH模型能够通过与单变量案例相同的方法被生成。在多变量GARCH(MGARCH)模型中,对于,条件协方差矩阵有以下形式:
(16.3.5)
这里,同样是系数矩阵。例如,对于一个二变量GARCH(1,1)模型,有
一个VARMA表示一个MGARCH过程将包含类似的单变量案例(参见16.2.7),通过定义
这里,当时,,当时,。这个代表案例经常是有用的,在得到MGARCH过程的特性时。(具体内容参见16.6.1)
Engleamp;Kroner(1995)在论文中谈到,MGARCH过程中,在16.3.5式中给定的关于的条件协方差是固定的,如果矩阵所有的特征根少于一个。
MGARCH模型的参数空间通常有很大的维数,并且需要很严格,以确保代表的独特性,并获得合适的条件协方差特性。为了减少参数空间,Bollerslev等(1988)讨论了对角MGARCH模型,这里,和都是对角矩阵。二者择一,一个有着以下形式的BEKK模型可能是有用的:
(16.3.7)
这里,是一个的三角矩阵,系数矩阵,同样是的。给定的相似模型MGARCH和VARMA模型,清楚地辣子第12章,12.1节,那个限制条件必须强加到参数矩阵上,以保证参数独特性。Engleamp;Kroner(1995)给了关于BEKK GRACH模型以下特性,这些特性同样处理了独立性问题:
(1)根据16.3.6的固定条件,BEKK模型被视作稳定的,如果矩阵所有的特征根
(16.3.8)
其模小于1.
(2)BEKK模型嵌套所有的GARCH模型正定对角矩阵,也就是说,每一个有着正定条件协方差矩阵的对角GARCH模型都有BEKK代表。
(3)BEKK模型(16.3.7)生成正定协方差矩阵,如果都是正定矩阵,而且如果至少矩阵中的一个是非奇异矩阵。(参见,Engleamp;Kroner(1995,命题2.5))。
(4)在BEKKGARCH(1,1)模型中,当时,以下陈述
是独立的,如果所有的对角元素是正的,并且。这里,分别表示和左上角元素。
(5)对一个更加一般的BEKK GARCH(1,1)模型,
唯一性是通过以下条件限制的:
(a)所有的对角元素都为正。
(b).
(c)在矩阵,第一个列和第一个行都为0。此外,矩阵右下角的元素均大于0。
(d)对于类似的限制,同样适用于。(参见,
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[145975],资料为PDF文档或Word文档,PDF文档可免费转换为Word


