变点识别：综述外文翻译资料

英语原文共 21 页，剩余内容已隐藏，支付完成后下载完整资料

变点识别：综述

摘要：当控制图处理失控情况时，应开始根本原因分析，以确定和消除过程中出现的特殊变化原因。变点是指过程中发生特殊原因导致其从控制状态偏离到失控状态的时间。在单变量和多变量过程中，确定变化点被认为是根本原因分析的重要步骤。如果一个变更出现在一个非正态分布的过程均值、方差或两者兼有的过程中，那么变点应该分别在过程均值、方差或两者中进行标识。本文试图对单变量和多变量正态过程对应的不同环境下的平均变化点的研究进行综合评述。

关键词：变点 单调 等分 反序 统计过程控制 软计算

1.导言

目前，统计过程控制（SPC）是质量专业人员最有力的方法之一。当质量工程师接触到统计过程控制时，控制图通常被用作一种有效的工具。控制图可以帮助质量工程师监控工艺参数并识别工艺的可变性。也就是说，控制图用于检测识别出的问题是由特殊原因还是常见的变化原因引起的。常见原因对应系统问题，特殊原因本质上称为非随机源。特殊原因会以两种不同的方式影响工艺参数。一种方法是移动参数，然后更改消失，并有可能在过程中再次出现。在这种情况下，识别失控状态被称为孤立的特殊原因。另一种方法是持续的特殊原因，在这种原因中，影响过程的变化会一直保持到检测到并消除为止。在这种情况下，新的条件会导致过程失控，并且在采取一些纠正措施之前，它一直保持不变。

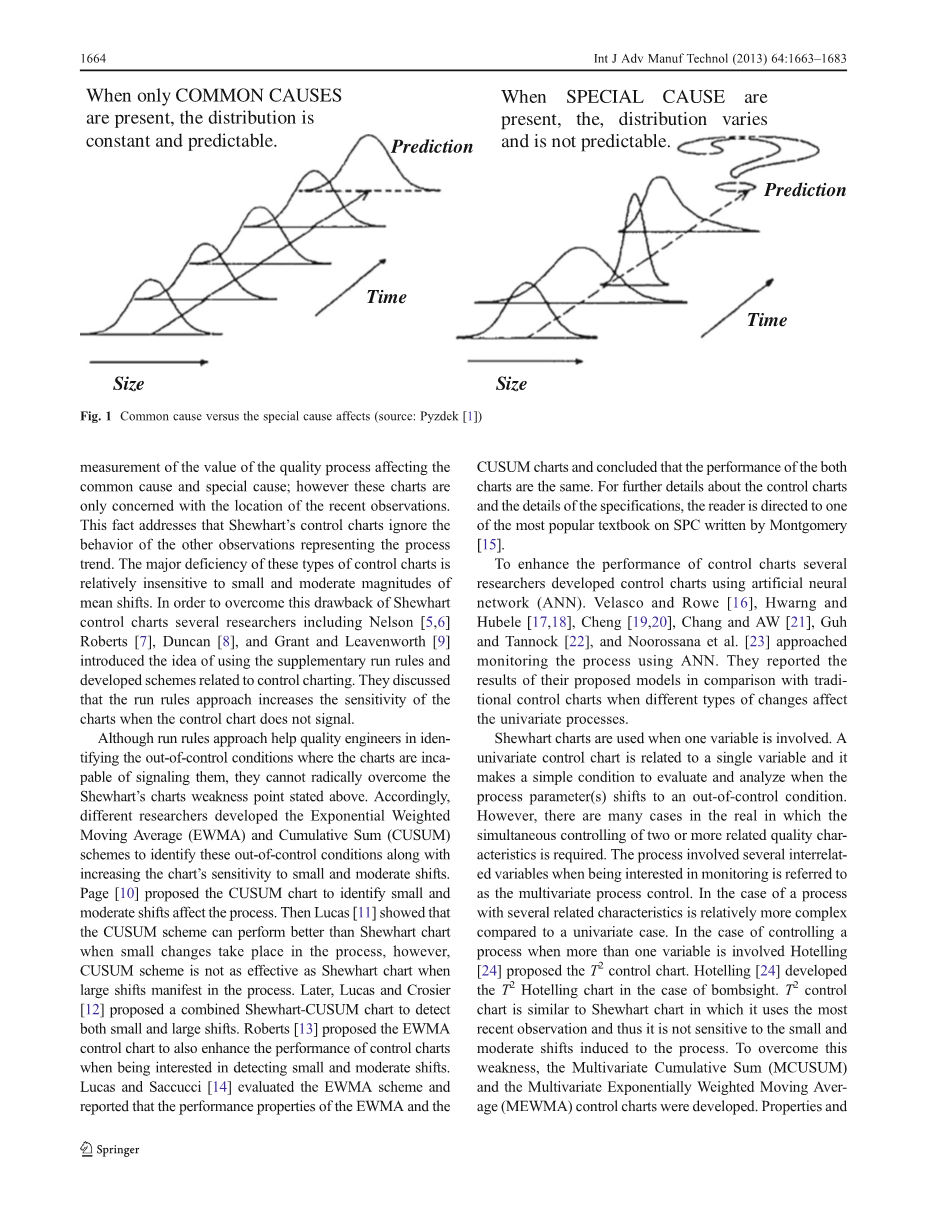
对于不同类型的观测数据，有不同类型的控制图来统计控制一个过程。因此，我们可以在文献中找到两大类控制图：（a）连续数据的可变控制图；（b）属性数据的属性控制图（见Pyzdek[1]；图1）。

图1 共同原因与特殊原因影响（来源：Pyzdek[1]）

1931年，Shewhart提出了一种新的质量方法，首次提到了控制图的应用。Shewhart[2]表明，一个过程的变化不能完全消除。对过程变化性质的新方法导致他计算了当过程在正常状态下运行时过程变化的极限。Shewhart方法中统计过程控制的基本规则是：当变量属于共同原因时，应将其释放到偶然的位置；当变量属于特殊原因时，应将其识别并消除。适当使用控制图的质量工程师可以按照美国材料试验协会（ASTM）[3]或美国国家标准协会（ANSI/ASQ[4]）引入的标准进行控制图。

在质量规范控制图的绘制领域，Shewhart的控制图被用来监控影响共同原因和特殊原因的质量过程值的测量，但这些图只涉及最近观察的位置。这一事实说明了Shewhart的控制图忽略了代表过程趋势的其他观察结果的行为。这些类型的控制图的主要缺陷是相对不敏感的小和中等程度的平均位移。为了克服Shewhart控制图的缺点，包括Nelson[5,6]、Roberts[7]、Duncan[8]和Grant和Leavenworth[9]在内的几位研究人员介绍了使用补充运行规则的想法，并开发了与控制图相关的方案。他们讨论了当控制图没有信号时，运行规则方法会提高图表的灵敏度。

虽然“运行规则”方法有助于质量工程师发现图表无法发出信号的失控情况，但他们无法从根本上克服上述Shewhart图表的弱点。因此，不同的研究人员开发了指数加权移动平均（EWMA）和累积和（CUSUM）方案来识别这些失控的情况，同时增加了图表对中、小位移的敏感性。第[10]页提出了CUSUM图表，以确定中、小位移对过程的影响。Lucas [11]表明，当过程中发生小的变化时，CUSUM图的性能优于Shewhart图，但当过程中出现大的位移时，CUSUM图不如Shewhart图有效。后来，Lucas和Crosier[12]提出了一个组合Shewhart-CUSUM图来检测小位移和大位移。Roberts [13]提出了EWMA控制图，以便在有兴趣检测中、小位移时提高控制图的性能。Lucas和Saccucci[14]评估了EWMA方案，并报告了EWMA和CUSUM图表的性能特性，并得出结论，两个图表的性能相同。关于控制图和规范细节的更多细节，读者可以参考蒙哥马利写的最流行的SPC教科书之一[15]。

为了提高控制图的性能，几位研究人员利用人工神经网络（ANN）开发了控制图。Velasco和Rowe[16]、Hwarng和Hubele[17,18]、Cheng[19,20]、Chang和AW[21]、Guh和Tannock[22]以及Noorossana等人[23]使用人工神经网络（ann）对过程进行了监测。当不同类型的变化影响单变量过程时，他们报告了与传统控制图相比所提出模型的结果。

当涉及一个变量时，使用Shewhart图。单变量控制图与一个变量有关，当过程参数转变为失控状态时，它使评估和分析成为一个简单的条件。然而，现实中有许多情况需要同时控制两个或多个相关的质量特征。当对监测感兴趣时，过程涉及几个相互关联的变量，称为多变量过程控制。对于具有多个相关特征的过程，与单变量的过程相比，要复杂得多。在控制一个过程的情况下，当涉及多个变量时，Hotelling[24]提出了控制图。霍特林[24]开发了霍特林图表，以防爆炸。控制图与Shewhart图相似，它使用了最新的观察结果，因此对过程中的小位移和中位移不敏感。为了克服这一缺点，开发了多变量累积和（MCUSUM）和多变量指数加权移动平均（MEWMA）控制图。随着时间的推移，包括Woodall和Ncube[25]、Healy[26]、Crosier[27]、Pignatiello和Runger[28]、Ngai和Zhang[29]、Chan和Zhang[30]、Qiu和Hawkins[31,32]、Runger和Testik[33]在内的许多研究人员对MCUSUM控制图的性质和性能进行了研究。包括Lowry等人[34]、Rigdon等人[35]、Yumin等人[36]、Runger和Prabhu等人[37]、Kramer和Schmid等人[38]、Prabhu和Runger等人[39]、Fasso等人[40]、Borror等人[41]、Runger等人[42]、Tseng等人[43]、Yeh等人[44]、Testik等人[45]、Testik和Borror等人[46]和Chen等人[47]在内的几位作者也对MEWMA控制图的制定做出了贡献。

多变量环境监测在实际案例中的重要性，以及在采用统计方法时对性能水平的限制，使得一些研究人员将重点放在软计算方法来监测过程。Zorriassatine等人[48]、Hwarng[49]、Guh[50]、Hwarng[51]使用基于人工神经网络的模型调查了过程监控，其中考虑了涉及多个变量的过程。此外，Guh和Shiue[52]使用决策树接近相同的条件。

在制造案例中，质量工程师在实践中控制和改进一个过程，可能会考虑与生产线相对应的顺序阶段。常见的条件也可以在服务系统中找到。包括几个阶段以产生输出的过程称为多级系统。与仅在一个阶段控制质量规范的情况相比，应采用不同的方法控制多级系统。一些作者对多级系统的近期控制进行了研究。石和周[53]和刘[54]回顾了在多级系统中控制和诊断变异传播到其他阶段的方法。

尽管在文献中可以找到不同的提议控制图来监控涉及一个或多个变量的过程，但这里的关键点是，这些控制图无论多么敏感，都无法在过程中首次出现变化时实时检测。换句话说，控制图发出失控信号的时间不是过程开始受到持续特殊原因或特殊原因集影响的实时时间。图表给出失控信号的时间仅表明过程中存在特殊变化原因。这意味着在图表触发失控状态信号之前，流程中发生了变化，图表无法立即检测到。当过程受到持续的特殊原因的影响并不可避免地偏离失控状态时，称为变点。变点与变更在过程中的实时表现有关。当质量工程师开始根本原因分析以检测和消除影响过程的特殊原因时，变点的识别对路线起着至关重要的作用。对于变化敏感的情况，触发失控信号的时间可能接近变化点。然而，在对变化不敏感的情况下，预期的信号时间将远离变化点。根据文献报告的结果，控制图被认为是无法有效识别变点的工具。因此，由于失控信号在某种意义上不应接近于变化点的值（相对于图表的灵敏度），因此信号是变化点的偏差估计量。当质量工程师专注于根本原因分析时，确定变点将有助于揭示变更的来源。对变点的了解将为调查特殊原因提供一个良好的开端，并可减少对失控情况负责的来源的错误识别的错误。

本文回顾了研究单变量和多变量过程的平均变化点及其统计和软计算方法的文献。

在下一节中，将介绍变点定义及其不同的特性和置信域。单变量和多变量环境的平均变化点方案分别在第3节和第4节中提供。最后，我们的总结性发言将在第5节中讨论。

2.变点定义

Pyzdek[1]讨论了在研究过程中分布的三个基本性质。Pyzdek[1]讨论了分布的位置、分布和形状。扩散是指分布的方差和标准差，而形状是指随后的分布模式，最后位置是指随后的分布参数，如平均值。这三个特性如图2所示。

图2 一个过程中的三个潜在变化

现在，假设是从一个过程中观察到的独立子群平均值序列。假设随机变量遵循已知的密度函数 ，其中表示参数空间。假设过程在时间之前处于控制状态，然后时间之后，一个变化会影响过程，并且过程切换到失控状态，并且在假设该信号不是错误警报的情况下，它将保持新状态，直到时间之后图表信号发出。因此，是受特殊原因影响的过程的观察结果。在这种情况下，时间点表示流程中首次发生更改的时间。在涉及多于一个变量的过程中，并且通过p相关质量特性的联合水平来测量过程，我们假设是独立的观测向量，其中遵循已知的p变量分布。

如果概率分布从变为，在过程中出现变化的时间之后，即在时间之后，则至少出现以下情况之一：

1. 已知随机变量在时间t后的概率分布不发生变化，但参数不相同。它意味着，但。

2. 已知时间变化后的概率分布和概率分布对应的不同参数。当时提供概念。

文献中所述的案例称为变化点，时间用变化点表示。在过程中发生实际变化后，失控信号的延迟时间如图3所示。变点识别使质量工程师有机会有效地进行根本原因分析，以识别和消除特殊原因。

例如，假设在控制过程中，单变量过程中感兴趣的质量特征遵循平均和方差的正态分布。如果在未知时间后，特殊的变化原因分别影响过程平均值或过程方差或两者都会导致变化值和/或，则得出结论：过程在时间时偏离失控状态。换言之，如果是指当前的子组，且，则可以得出结论，工艺在控制条件下运行，参数尚未改变。这种情况可以表述如下：

(1)

Samuel[55]给出的示例有助于认识变化点的概念意义。他们认为这是一个锻造活塞环的过程，活塞环的外径是应该监控的质量特征。在这个数值例子中，环的外径是100毫米。然后，当过程处于控制状态时，质量特性的平均值等于100。工艺标准差为，子群尺寸为。在这种情况下，Shewhart控制图的UCL和LCL分别等于107.5和92.5。子组的平均值如表1所示。

表1 变点的子组平均值示例

您可能感兴趣的文章

• 基于一个幂GARCH模型对黄金市场的研究外文翻译资料
• 主成分分析教程外文翻译资料
• 逐步回归的显著性检验外文翻译资料
• 大数据挖掘：回顾外文翻译资料
• DSSAE-BBOA：基于深度学习的气象大数据分析和可视化外文翻译资料
• 使用G或K点模式空间统计的统计推断外文翻译资料
• 李代数的扩张结构外文翻译资料
• 灾民居住偏好转变：以2016年日本熊本地震后益城三波面板数据为例外文翻译资料
• 影响印尼证券交易所投资的因素-增进对资本市场的了解外文翻译资料
• 基于JMP的教育数据挖掘外文翻译资料