
英语原文共 12 页,剩余内容已隐藏,支付完成后下载完整资料
采用滑动时间相关方法研究数值模式的可信计算时间
刘勇、王鹏飞、黄刚
摘要:本文采用滑动时间相关分析方法,研究了两种典型的混沌数值模型(Lorenz系统和Chen混沌系统)的预测时间(PT)和大气环流模型(ECHAM5)的可信计算时间(RCT)。通过各种数值实验,结果表明,STC方法检测到的Lorenz系统(和Chen混沌系统)的最大预测时间与传统误差限方法一致,说明STC方法的有效作用。然后,以位势高度为例,探讨了ECHAM5的RCT和积分时间步长、初始条件、模型分辨率等潜在影响因素。结果表明:(1)RCT的高价值区域主要位于热带地区,且全球平均RCT(GMRCT)随时间步长增加而减少:(2)海洋强迫可以增大RCT平均值在南半球(SH)和北半球(NH)的差异,这意味着在NH的RCT比在SH对计算误差更为敏感;(3)从冬季开始强迫比从夏季开始,模型的RCT(GMRCT)表现出更显著的季节特征,累计时间较长(约1-2天);(4)高分辨率(T106) ECHAM5的RCT与低分辨率(T63) ECHAM5的RCT具有相似的空间特征,但GMRCT和半球差异减小。
- 引言
数值模型的可预测时间(PT)或可信计算时间(RCT),简单地定义为由于算法的截断误差和浮点计算的舍入误差导致模拟结果中的误差逐渐增大直至达到规定阈值的时刻。以前的研究表明,一些非线性系统即使初始值完全准确,由于舍入误差的存在,系统的结果也仍然存在最大RCT (Li et al. 2000;Teixeira等人,2007;Liao2009)。例如,他们指出Lorenz系统(LEs)在双精度计算下的可预报时间约为35个时间单位(TU)。对于更复杂的数值模式,如大气环流模型(AGCM)和天气预报模型,初始值和算法/舍入误差都会影响模型的RCT,并进一步限制了模型的预测/模拟能力。因此,数值模式的RCT不仅是一个数学问题,也是评价模型性能的一个重要因素,具有重要意义和研究价值。尽管有一些研究关注于数值模式的可计算性(Wang et al. 2009; Song et al. 2012), 但是关于这类模型(AGCM或天气预报模型)具体的RCT以及模型RCT的估计方法尚不清楚,需要进一步研究。
一个数值模型的PT/RCT与其动力学系统的PT/RCT及其误差增长规律密切相关。Lyapunov指数是描述一个混沌系统初始误差平均增长速率的常用方法,广泛用于研究混沌动力系统的特性(Oseledec 1968)。在混沌系统研究中,如果初始误差是delta;0和允许的最大误差是Delta;(称为:误差限),最大Lyapunov指数lambda;max可以用来定义混沌系统的可预报期限 (Eckmann and Ruelle 1985;Wolf等人1985;洛伦茨1996)。Tp ~ 1 /lambda;maxln(Delta;/delta;0)。然后将Lyapunov指数扩展到局部Lyapunov指数(Yoden和Nomura 1993)和非线性局部Lyapunov指数(NLLE) (Ding和Li 2007a, b;丁、李2012;李、丁2011),用于研究混沌系统的局部动力学特征。NLLE是近年来新发展出来的一种方法,能够利用原始方程估计平均误差增长率和误差饱和特性,可用于研究实际天气和气候系统的可预报性。
误差限(Delta;)是一种用来揭示RCT/ PT用于线性和非线性Lyapunov指数的方法。为了方便,我们通常使用误差增长曲线而不是Lyapunov指数来估计动力系统的RCT /PT。首先,我们通过数值实验或其他方法获得生长曲线误差,然后找出误差delta;(delta;0 lt;Delta;)到达Delta;的第一个时刻,即RCT/ PT。对于不同动力系统,选择合适的Delta;往往决定了真正的解。Delta;避免了解的这种依赖性,相对误差的方法是采用一些研究(Li et al . 2000;Wang et al. 2006;Liao 2009;Liao 和Wang 2014)。例如,Liao(2009)应用Delta;相对误差5%,引入另一个极限u1 * u2 lt;minus;ε(εgt; 0,u1和u2表示同一个变量的趋于不同的解)有RCT/ PT。NLLE研究RCT的标准更加复杂。在非线性动态系统中,我们经常选择Delta;= 95%(为饱和误差)。在我们得到RCT/PT之前,我们需要先计算,但是计算需要足够的样本,非常耗时。
上述误差限方法可以应用于对一个动力系统的RCT/PT的整体和局部的单变量研究。此外,小的delta;0,数值模拟和理论的相关分析结果证实,基于上述方法的一个动态系统的RCTs显示相似的结果,和RCT/ PTs的个体变量和整个系统非常接近。针对上述方法费时、系统依赖等局限性,本文提出了一种简单实用的时间滑动相关法(STC),用于研究动态系统的RCT/PT和复杂AGCM;下面将介绍STC方法的简介和优点。
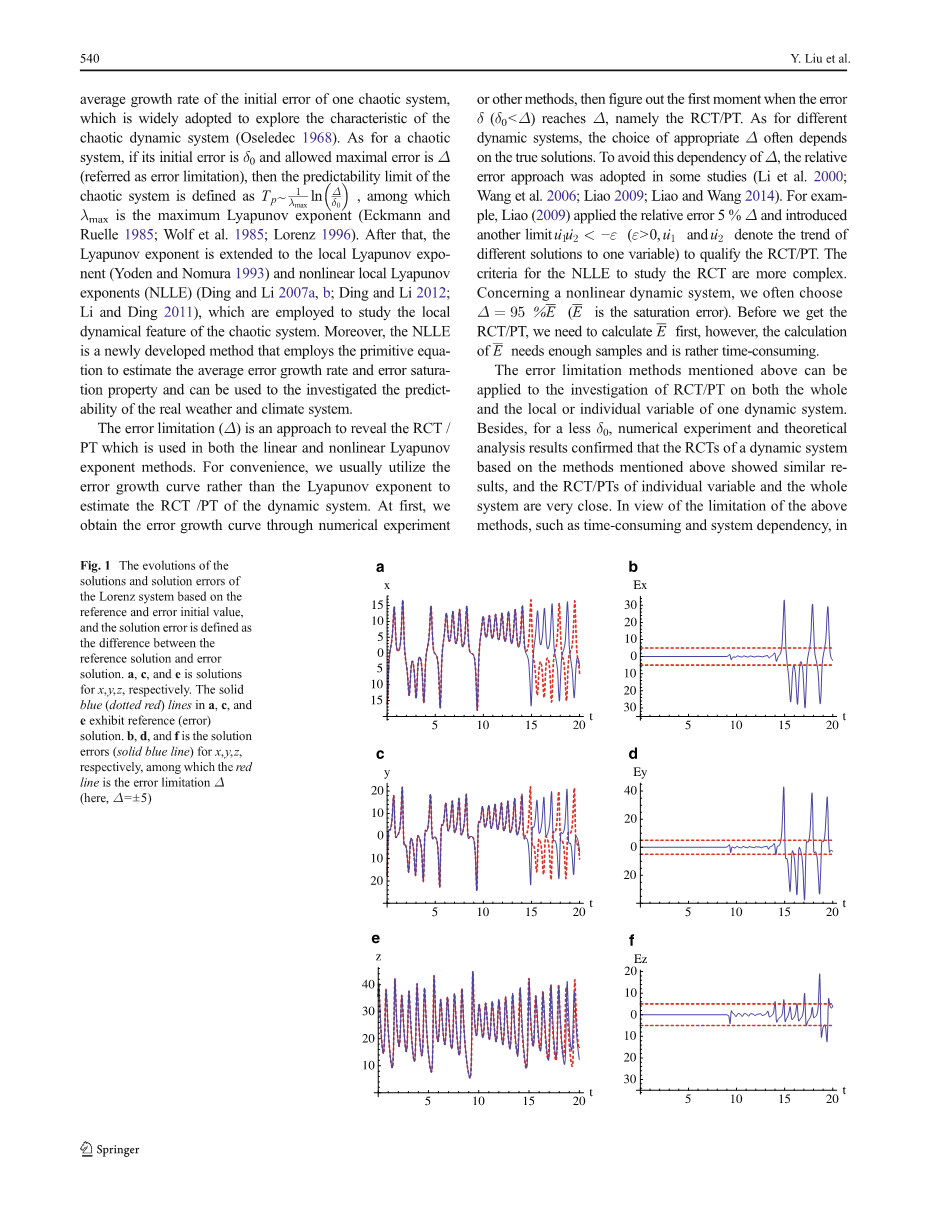
图1.基于参考和误差初值的Lorenz系统解和解误差的演化,由于解误差的不同分别定义为参考解和误差解。a,c,e分别是x ,y, z的解。a、c和e中的纯蓝色(红虚色)显示参考(误差)解。b、d和f分别x,y,z的解误差(蓝实线),其中红线是Delta;误差限(此处Delta;= 5)
图2. STC在参考解和误差解之间的演化过程。a x,b y, c z,水平虚线表示对应99%置信水平的参考值,垂直虚线表示STC第一次达到参考值
- 方法原理
相关分析方法是一种常用的方法,被广泛用于研究两个样本之间的关系,无论这两个样本是线性系统还是非线性系统。STC基于常用的相关方法,假设有一个滑动窗口,常用于研究两个时间序列之间关系的变化。两个时间序列之间关系的显著性可以通过定信度水平为双边的t检验来检验,对于一个给定的置信度,如99%,可以根据STC的演化来实现它们关系的过渡时间或时间跨度。通常,STC被用于研究两个不同的时间序列或两个不同的动态系统之间的关系。而如果我们将其应用于两个相似的时间序列x, y, y与x相同但有初始误差时,STC可以被认为是误差时间序列与参考时间序列之间的联系,从而进一步研究RCT。此外,我们还引入了初始误差相对较小的极限,参考时间序列与误差时间序列的相关性接近于1;当误差达到饱和时,相关性接近于零。而由于样本数量和滑动窗口的限制,我们选择计算STC,当STC第一次超过置信水平时,定义为RCT。这些准则适用于一般的数值模型。而且与误差限方法相比,STC方法具有以下优点:(1)可用于研究线性和非线性动力系统的RTC;(2)避免了在使用误差限制方法时,由于单点误差剧烈扰动是可信计算时间判断失误;(3)不需要使用绝对误差,无需提前估计解域,也不需要预先获得饱和误差。
接下来,我们将使用STC方法来研究它在动态系统RCT/PT检测中的有效性。首先采用STC方法和误差限制方法对常见的混沌动力系统进行了PT检测,然后采用STC方法对某一气候数值模型的RCT/PT进行了研究。需要注意的是,下面提到的STC表示来自相似数值模型结果的两个样本之间的相关性,但初始误差(或初始值相同,但不同的参数,如不同的时间步长、初始条件等)。
图3.是STC和解误差基于实验初始误差delta;0= 10 - 6的解曲线。a-c与图2 a-c相同,d -f显示的解误差与图1b、d、f相同
图4. a. K=666洛伦兹系统的Tc-M图,直线Tc=3M。b.洛伦兹系统的Tc- k图,M=32,直线Tc=0.75K-7.5。这里的精度是二进制位。三角形(虚线)表示误差限(STC)方法的结果
图五.同图三,但是对Chen系统,令初始误差delta;0= 10 - 5
图六.同图五,但初始误差delta;0= 10 - 6
- 混沌动力系统的可预报时间
本节选取常用的混沌系统Lorenz系统和Chen系统为例,利用STC和误差限方法检测它们的可预报时间(PTs)。
3.1 Lorenz系统
式1为Lorenz系统(Lorenz 1963),其中、r、b为无量纲常数,分别为28.0、10.0、8/3,t为无量纲时间(单位:TU)。对洛伦兹系统进行了三次不同初始值的数值实验,得到了参考解和误差解。x的引用初始值xo,yo,zo 是-15.8,-17.48,和35.64, xo,yo,zo的其他两个初始误差和参考值的是相似,但以更少的干扰delta;0=10-5和delta;0=10-6 乘 xo,yo,zo 。
(1)
图七.同图四,但是是Chen系统
基于误差限理论,混沌系统的可预测性极限定义为Tp ~(1 /lambda;max)* ln(Delta;/delta;0),这里的PT为(1/0.906)* ln(5/10-5)= 14.5 TU。至于实验结果,参考解和错误解的x,y,z差异都绘制在图1。x的参考解和误差解在图1 a - b,显示15 TU之前没有明显的差异,和Fig.1bDelta;=plusmn;5,实验结果表明,x的PT是14.7 TU。y的参考解和误差解的特征与x相似,实验得到的PT为14.1 TU。至于变量z,参考解和误差解的特征没有x,y显著,和误差时间序列图1 f,我们可以知道z的PT为13.9TU。每个变量的PT数值实验结果和Lorenz系统的理论分析得到的PT是一致,并且数值实验的整体PT也接近基于理论分析的PT(数据未显示)。
现在,我们利用STC方法,在参考解和误差解的数值结果的基础上,研究了洛伦兹系统的PT。这里,滑动窗口定义为20个时间间隔(1个时间间隔为0.1 TU),2 TU。图2分别给出了x、y、z的参考解和误差解STC的演化过程。根据给定信度水平为99%的t检验,x,y,z的PTs分别为13.9 TU, 13.9 TU, 21.0 TU。变量x,y的PTs非常接近理论分析(14.5 TU)和Delta;检测(14.7 TU,14.1 TU)。然而,STC方法所获得的可预报时间是不同于理论分析和Delta;检测。从图1e和2c可以看出,z的参考解和误差解具有相似的演化特征,且STC变化缓慢,因此统计的PT更长。由于Delta;检测方法服从动力系统获得PT,STC方法是更高倍的获得数值模式中的PT的一种统计方法,因此从单个实验获得的PT和理论分析与Delta;检测方法的具有差异性是可以接受的。
其他相似实验都是基于初始误差为delta;0=10-6,对应的理论可预报时间约为17.0 TU。STCs和参考解与误差解的差异见图三。由STC方法检验算出x,y,z的可预报时间分别为17.5TU,17.2 TU,和17.0 TU,有误差限 Delta;方法求得的可预报时间为17.7 TU,17.1 TU和16.9 TU。见(图3d-f)。两者的结果都和理论结果吻合。
由于STC方法能够揭示两个时间序列之间相关关系的演化,因此也可以用来检测由数值误差引起的动态系统的RCT。例如,Liao(2009)采用400阶泰勒级数和800位有效数字的数学程序的clean数值模拟方法得到了1200 TU的结果。此外,Liao(2009)提出了得到泰勒方法(M)的阶数与Tc之间关系的实验方法(可靠的计算时间有时被称为临界计算时间,我们将其缩写为Tc)。因为这种类型的计算没有初始误差delta;0,因此我们可以将其与初值误差的可预报时间问题看成是不同的问题,但是判定到达阈值的方法是一样的,仍然可以使用误差限的的方法。所以当我们研究Tc,我们仍然可以使用Delta;= 5误差限标准。研究Tc的数值算法可以在Liao(2009)和Wang et al.(2006, 2012)中找到。通过应用这种方法,我们首先保持精度,例如,K = 666和更改命令为M =20minus;100(间隔10),然后我们可以根据M获得每个Tc,我们称之为Tcminus;M图。其次,我们M = 32为常数,使精度不同,如K =50-200(间隔10)获得Tc-k图。
结果表明,STC可以获得同误差限制(Delta;= 5)方法一样的正确的Tc -M和Tcminus;K图(图4)。正确的Tc M和Tcminus;minus;K图是基本分析计算参数获取可信计算时间导致[1,Tc],和这些参数对洛伦兹系统的长时间模拟具有指示意义。
3.2 Chen系统
Chen和Ueta(1999)记录了Eq.2中描述的另一个混沌系统,其中a=35,b=3,c=28。在3.1节中,我们进行了三个实验获得(x, y, z)解包括一个使用初始值的参考实验(xo,yo,zo ) =(-3,2,20)和两个引入初始值作为参考的对比实验,但以误差delta;0=10minus;5 和 delta;0=10minus;6 分别乘相关数值。
应用STC和误差限方法对Chen系统的可预测时间进行了研究。相对对比试验初始误差delta;0=10minus;5 (图5),由STC方法检验到的可预报时间(x,y,z)(图5 a - c)分别为5.3TU,5.3TU,和8.3TU,由误差限方法得到可预报时间分别为6.2TU,6.1TU,和7.6TU。差异在1TU。当初始误差为delta;0=10minus;6 (图6),由两种方法检测(x,y,z)的可预报时间非常接近,由STC方法得到7.5TU,7.5TU,和7.6TU,见(图6 a - c)和误差限方法得到7.5TU,7.5TU,和7.5TU。此外,随着初始误差的减小,两种方法检测的PTs值也越来越接近。从图3和图6可以看出,Lorenz系统的PTs比Chen系统的PTs要长;这是因为洛伦兹系统的Lyapunov 指数大于陈氏系统的Lyapunov 指数。
图7中的结果
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[18371],资料为PDF文档或Word文档,PDF文档可免费转换为Word


