
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
优化可见光谱中的高效抗反射涂层的二维薄硅柱阵列
JulienProust1,Anne-LaureFehrembach1,Freacute;deacute;ricBedu2,IgorOzerov2和NicolasBonod1
在硅晶片表面上每间隔100nm蚀刻100nm*140nm的正方形晶格时,光反射会显著减少。纳米结构设计的优化是为了扩大抗反射涂层在可见光谱上对两种基本极化的光谱容限。角度和极化分辨光学测量显示,当在宽角度范围内的两个极化的可见光谱中平均测量时,光反射保持在5%以下。即使在倾斜入射时,光反射对偏振仍然极不敏感。
在不同物质之间的界面处发生的光反射是由于折射率不同造成的阻抗失配。光反射取决于两种物质之间的入射角、光偏振和对比度,这些材料被定义为折射率之间的差异。在各种材料中,硅和玻璃在光学(玻璃)和光电子(硅)中的应用引起了很高的注意。硅与空气的光学对比度在可见光和近红外光谱中约为2.5,这导致了强烈的反射。这种现象降低了多种光电元件,如CCD、CMOS传感器和光伏电池的效率。目前已经提出了不同的策略来设计抗反射涂层。首先提出了一种薄电介质涂层,对于给定的一组参数如入射角和频率,增加第二个界面,导致两个反射光束之间的相互干涉。薄电介质多层导致在垂直于界面的方向上构建一维结构。另一种策略主要是用二维平面纳米结构构建界面。这种方法的优点在于不需要不同材料,纳米结构的多功能形状能为更好的性能提供额外的优化参数。目前已经提出了多种二维纳米结构来设计抗反射涂层,例如纳米线,纳米穹顶或纳米纤维。仿生阵列的灵感来自于昆虫复合眼睛的几何排列和硅颗粒的双周期阵列,这是第一个用于设计抗反射涂层结构的设计。在不透明金属薄膜的前后界面上添加双周期阵列,可在给定频率下产生高透光率。Lalanne和Morris于1997年提出了一种高效的硅颗粒抗反射涂层。通过使用光束光刻技术,他们构造了100纳米厚的纳米硅层,这种纳米硅层在宽光谱范围内的光反射剧烈减弱,并且对光偏振的灵敏度非常弱。最后,纳米压印技术被用于蚀刻纵横比约为1和周期为450nm的硅颗粒。单个硅Mie谐振的谐振特性和由于电磁多极共振的激励而产生散射特性被格外关注。共振散射体是设计薄抗反射涂层的优良方法。承载局部表面等离子体激元的金属微粒可以添加到高折射率层以增强不同光学材料之间的光透射。最近,通过界面控制光反射和透射,越来越多的全硅表面领域引起了人们的兴趣。值得注意的是,设计良好的硅纳米盘构成的全介电质交换表面可以在任何入射角、频率和极化下产生布鲁斯特效应,即零反射光。
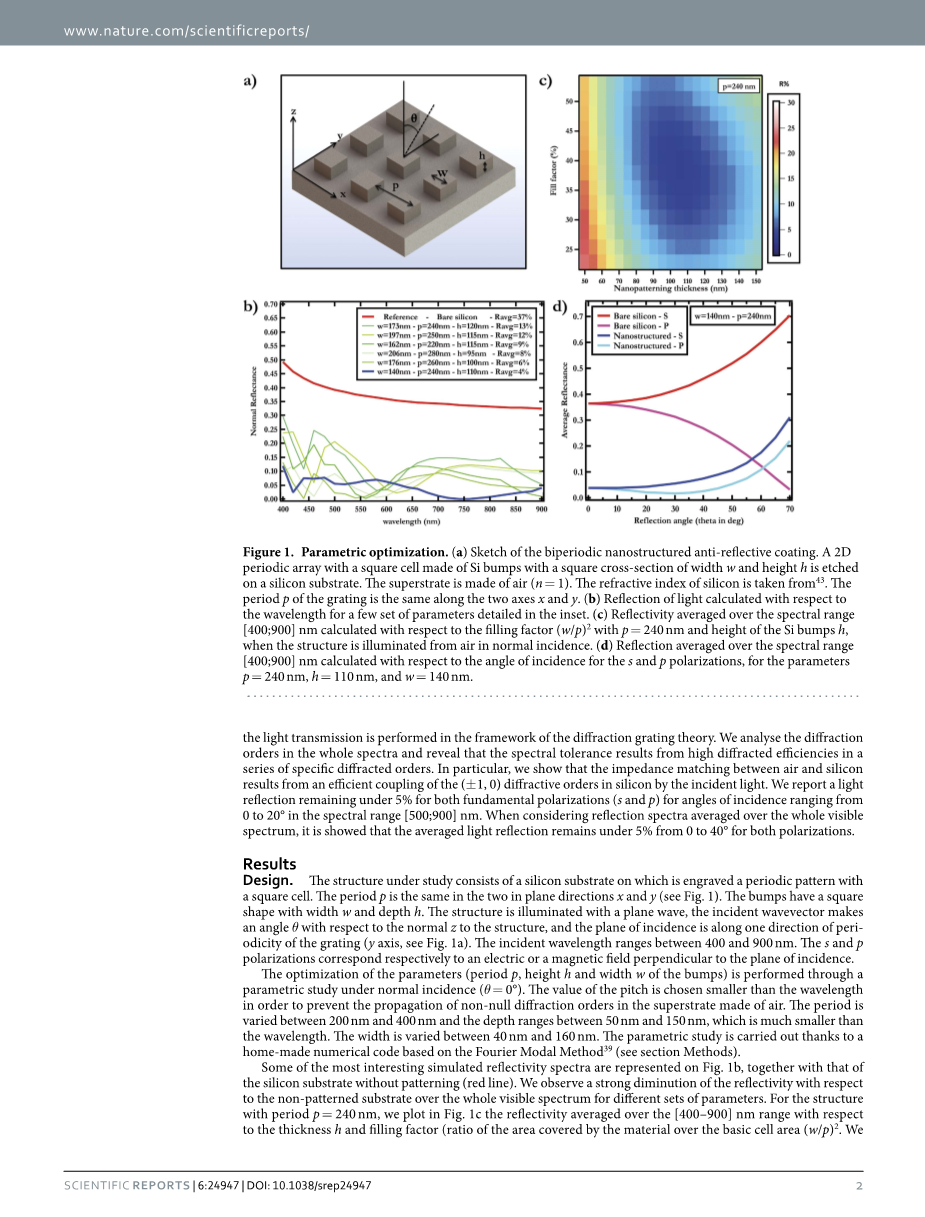
图1参数优化
(a)双周期纳米结构抗反射涂层模拟图。在硅衬底上蚀刻具有由具有宽度w和高度h的正方形横截面的Si凸块制成的正方形单元的2D周期性阵列。顶层是由空气构成的(n=1)。硅的折射率取自43。光栅的周期p沿着两个x轴和y轴是相同的。
(b)根据插图中详述的几组参数计算波长的光的反射。
(c)当在正常情况下从空气中照明结构时,在相对于p=240nm的填充因子(w/p)2和Si凸块h的高度计算的光谱范围[400;900]nm上的平均反射率发病率。
(d)对于参数p=240nm,h=110nm和w=140nm,在相对于s偏振和p偏振的入射角计算的光谱范围[400;900]nm上的平均反射。
这里我们会关于在整个可见光谱范围内具有宽容差的抗反射薄蚀刻硅层的设计、制造和表征作出报告。我们假设硅纳米柱的截面为宽140nm、厚110nm的正方形横截面,这种结构具有高光谱容差和对入射偏振的弱依赖性。分析光传输是在衍射光栅理论框架内进行的,我们分析了整个光谱中的衍射级数,并发现了光谱容差是由一系列特定衍射级的高衍射效率引起的。而且我们发现,空气和硅之间的阻抗匹配是由入射光在硅中的(plusmn;1,0)衍射级的有效耦合引起的,在[500;900]nm光谱范围内,0到20°入射角的基本极化(s和p)光反射均保持在5%以下。实际上,考虑到整个可见光谱上的平均反射光谱,两种偏振从0到40°的平均光反射均保持在5%以下。
设计结果
设计方案
研究中的结构由一块硅基板组成,在基板上刻有一个正方形单元的周期性图案。周期p在平面方向x和y上是相同的(见图1)。凸块为具有宽度w和深度h的正方形形状。该结构被平面波照射,入射波向量相对于结构的法向z形成一个角度theta;,并且入射面沿着光栅周边的一个方向(y轴,参见图1a)。入射波长介于400和900nm之间。s和p极化分别对应于垂直于入射平面的电场或磁场。
通过垂直入射角(theta;=0°)下的参数研究来优化参数(周期p,高度h和隆起宽度w)。为了防止由空气覆盖层中的非零衍射级的传播,选择节距的值小于波长。周期在200nm和400nm之间变化,深度范围在50nm和150nm之间,远小于波长,宽度在40nm和160nm之间变化。基于傅立叶模态方法的自制数字代码进行参数化研究(参见方法部分)。
图1b显示了一些最有趣的模拟反射光谱,以及没有形成图案的硅衬底(红线)。对于不同的参数组,我们观察到在整个可见光谱上,非图案化基底的反射率有很大的减小。对于周期为p=240nm的结构,我们在图1c中绘制了在[400-900]nm范围内相对于厚度h和填充因子的平均反射率(材料覆盖在基本单元上的面积比面积(w/p)2可以看出,对于接近w=140nm和h=110nm的参数,获得可见光谱中的最小反射率(平均4%)。
由于空气制成的覆盖层与可见光谱中具有光学损耗的硅之间的近乎完美的阻抗匹配,因此硅是黑色的。参数优化以法向入射进行,但最终我们在图1d中绘制了针对优化结构(p=240nm,w=140nm,h=110nm)在400-900nm范围内平均的反射率对于s偏振和p偏振(入射平面包含光栅的一个周期性方向),极化入射角theta;。我们观察到,设计的抗反射涂层对于theta;显示出高耐受性,并且非常重要的是对极化的依赖性非常弱。对于两种极化,裸硅的反射率也在图1d中表示。
图2黑色硅
(a)裸露和纳米结构硅的光学图像(参数参见图1d)。
(b)防反射涂层的扫描电子显微镜图像(倾斜角度为65°),其由正方形电池的高度为110nm的方形硅颗粒的二维周期性阵列组成。
制造。通过电子束在1厘米times;1厘米大(100)取向的单晶硅晶片(250-300微米厚)上制造抗反射涂层。目标形状是一个方形的硅凸块阵列,深度110nm,周期d=240nm,宽度w=140nm,导致100nm的间隙。使用20kV加速电压,在用电子束(Pioneer系统,Raith)以约150mu;C.cm-2的剂量曝光之前,首先旋涂65nm厚的电子束正型光致抗蚀剂(PMMA)。显影后,20nm的镍层被蒸发以形成掩模。未受保护的区域通过由气体混合物(SF6-O2)步骤和纯O2等离子体暴露步骤组成的运行进行蚀刻。蚀刻目标硅厚度需要多次运行。镍掩模用FeCl3的酸性水溶液除去,样品用去离子水冲洗并在氮气流下干燥(参见方法章节)。最后,纳米结构的硅在纳米结构区域呈现黑色(见图2a)。扫描电子显微镜揭示了硅凸块的形状和晶格(见图2b)。
表征。在自制的共聚焦显微镜中观察裸露和纳米结构的硅样品的反射光谱(参见方法部分)。使用Glan-Thompson线偏振器对稳定的卤素灯光束进行偏振照射样品(见图3a)。照明光束放置在可围绕样品旋转的测角仪上。样品也可以围绕其轴旋转,使我们能够控制入射光束在样品上的入射角theta;,并收集反射光束(参见图3a和剖面方法)。样品反射的光通过times;20Mitutoyo显微镜物镜收集,数值孔径为0.4,工作距离20mm,与200mm焦距镜筒一起工作。反射光束用位于样品共焦位置的105mu;m芯光纤进行空间滤波,然后插入光谱分析仪(参见图3a)。使用此设置,可以针对s和p极化的入射波长和入射角测量样品的反射光谱。
用白色光源照射样品时用共聚焦显微镜获取的图像在图3b中针对不同入射角显示。可以看出,样品在15°以下的入射角度出现黑色,并且入射角到达40°时仍保持一定暗度。图3c显示了三种不同角度(theta;=20°,theta;=40°,theta;=60°)下测得的反射光谱的s和p偏振态以及裸露和纳米结构硅涟。首先可以观察到,即使对于高入射角,反射光谱仍然对偏振几乎不敏感。正如所料,p偏振体硅的反射随着入射角而减小,因为它在布儒斯特入射角接近74°时为零。在整个光谱上反射平均,对于块体和纳米结构硅(Rmoybulk和RmoyNP),两个极化由箭头表示。可以观察到,即使对于高入射角(60°),RmoyNP仍然始终小于Rmoy体积。在所需区域中的抗反射涂层的高效率通常在相机和光伏电池的theta;=[0;40°]范围内是显著的。而对于theta;=20°,光谱范围[500;900]nm以内,两个偏振的光反射均保持在5%以下(而裸硅约为30%)。
图3.光学特性。
(a)用于监测样品对(i)偏振,(ii)入射角和(iii)频率(见方法部分)反射率的实验装置草图。
(b)不同入射角的样品的光学图像。
(c)在三种入射角(从左到右:20°,40°,60°)下,针对裸露和纳米结构硅的s和p极化的波长的函数测量的反射率。
讨论
通过绘制光谱范围[400;900]nm内平均入射角的反射率来研究反射光谱对入射角的依赖性(参见图4)。对裸露和纳米结构的硅以及s,p极化,在可见光谱上测得的平均角度依赖性与通过傅立叶模态方法获得的数值结果进行比较。在4种配置(裸露和纳米结构硅,s和p极化)中观察到实验谱和模拟谱之间的显著一致性。薄抗反射涂层极大地减弱了裸硅对极化的强依赖性。在原始硅的情况下,由于布儒斯特入射角接近74°,光反射随入射角theta;在p偏振态下减小,而在s偏振态下随着theta;增加而增加。由于可以观察到对于两种极化而言光反射趋于平稳地随theta;增加,所以添加到裸硅上的非常小的凸起和非常薄的凸起消除了这种趋势。这项研究的关键结果是,在可见光谱上平均的光反射在p偏振的[0;55°]范围内和在s偏振的[0;40°]范围内保持在7.5%以下。这种宽的光谱容差以及对入射偏振的非常弱的灵敏度可以简单地通过纳米结构硅获得,而无需额外的薄膜涂层。硅结构化的厚度可以通过减小结构化的间距和增加硅柱的填充因子来进一步降低。
为了更深入地了解抗反射涂层的宽光谱容差的起源,我们计算了垂直入射时与基板中每个传播顺序相关的能量。我们首先在图5a中显示了光谱相对于立柱高度平均的传输效率,其中衬底中的每个传播顺序(由Si制成)的贡献。表示为(m,n)的顺序对应于倒数向量m2pi;/px n2pi;/py。我们绘制在整个频谱上平均占优势的(0,0)阶,然后添加不同的传播顺序以突出它们对传输能量的独特贡献。标记为s1的曲线是(0,0),(0,plusmn;1)和(plusmn;1,0)阶的总和,s2是考虑到(plusmn;1,plusmn; 1)阶,则s3为(0,plusmn;2)和(plusmn;2,0)阶,s4为(plusmn;1,plusmn;2)和(plusmn;2,plusmn;1)阶。我们可以看到,对于h=110nm观察到的高光谱平均透射主要来自(0,0),(0,plusmn;1),(plusmn;1,0)和(plusmn;1,plusmn;1)阶。我们还可以注意到,近乎完美的传播是由(0,0)到(plusmn;1,plusmn;2)和(plusmn;2,plusmn;1)之间的所有传播顺序的贡献产生的。我们还在图5b中绘出了相对于h=110nm的波长的传播顺序s1,s2,s3和s4的不同和,以及仅仅(0,0)阶以及(0,plusmn;1)和(plusmn;1,0)仅仅阶数和(plusmn;1,plusmn;1)阶数。这使得我们可以看到(0,0)阶在光谱范围[700nm;900nm]中占优势,(0,plusmn;1)(plusmn;1,0)阶在[500nm;700nm],而高阶(plusmn;1,plusmn;1)允许在450nm和600nm之间的波长实现高透射率。这些结果表明,这种纳米结构抗反射涂层的光谱容限是由不同传播级光谱中的一系列最大值引起的,最低级在光谱的红色部分占优势,在蓝色部分的最高级。
图4.光谱平均反射率的角度依赖性
作为s(蓝色三角形)和p(绿松石圆)极化的入射角的函数,在光谱范围[400;900]nm上测量的平均反射率。与裸硅比较,s(红色方块)和p(粉红色三角形)。虚线的彩色线条:模拟结果。灰色虚线:平均反射率,裸硅顶部,结构硅底部。
图5.模拟传输效率
(a)相对于以nm为单位的支柱高度h在光谱上平均的传输效率。实线:反射(蓝色),透射(绿色),反射 透射(红色)效率。虚线:(0,0)阶的传输效率,s1:(0,0),(0,plusmn;1)和(plusmn;1,0)阶,s2:s1 (plusmn;1,plusmn;1)阶,s3:s2 (0,plusmn;2) (plusmn;2,0)阶,s4:s3 (plusmn;1,plusmn;2) (plusmn;2,plusmn;1)阶。
(b)对于h=110nm,以nm为单位的波长lambda;的传输效率。
总之,我们报告了由薄纳米结构硅膜制成的高性能抗反射涂层的设计,制造和光学表征。纳米结构由140nm宽的正方形硅柱和240nm正方形晶格组成。这种设计不需要额外的薄膜涂层。在可见光谱范围内的宽光谱容差与非常弱的光偏振依赖性和由结构化硅晶片产生的准全向光吸收相关联。
方法
数值计算。该结构的数值建模采用基于傅里叶模态方法的数字自制代码进行。这个数字代码包括S-Matrix算法,以避免积分过程中的数值污染以及傅里叶级数的因式分解的正确规则。这个方法的详细描述可以在参考文献中找到。参数(周期p,凸块高度h和宽度w)的优化通过垂直入射(theta;=0°)下的参数研究进行。硅的折射率取自参考文献43(Palik, E. D. Handbook of optical constants of solids vol. 3 (Academic press, 1998))。在每个方向上,数值方法与傅里叶系数数量的收敛性被检查,并显示对于25个傅里叶级数达到了足够的数值精度(从-12到12)。当处理有损半无限介质时,作为由Si制成的衬底,传输效率必须按照纳米线层上方和下方表面中的坡印亭矢量流的比率来计算。这可以通过计算柱上方和下方的场的傅里叶分量来完成,即在z=0-,z=h 42处。
lt;
全文共7558字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[15615],资料为PDF文档或Word文档,PDF文档可免费转换为Word


