
英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
土工合成材料加筋土坡中影响峰值张力分布的因素
G. Tiwari bull; N. K. Samadhiya
摘要:本文提出了一种基于数值参数的研究方法,用以调查在边坡回填土中土工合成材料加筋层的张力及其剪切应变的分布。文献提出了关于沿边坡最大张力的位置的不同观点。很少有研究人员认为张力出现在坡脚,而多数研究人员认为其出现在边坡的中高处。为了解决这个问题,土工合成材料加筋土边坡的数值模拟采用有限元程序进行。因为这些参数对沿加筋层变化的峰值张力的位置和大小的影响,边坡倾角,回填土的性质,土工合成材料的性质和坡顶附加压力是不同的。这项研究揭示了边坡加固中峰值张力的位置和大小取决于几个参数,最重要的是边坡倾角,加筋层间距和边坡上的附加压力。在所有情况下,峰值张力的位置与由于沿破坏面的高剪切应变集中导致的潜在破坏面的位置一致。
关键词:加筋边坡 峰值张力 峰值张力的位置 参数研究 有限元分析 数值研究
导论
土工合成材料加固的边坡基本上是压实的填充路堤,其包含排列在水平面上的土工合成拉伸筋材。跨越临界破坏面时,抗拉筋材与土体保持在一起,以确保边坡的稳定性。在加固过程中,沿着边坡高度产生的这些力的分布非常不均匀。大多数设计问题遵循三角形模式,假定在边坡顶部的土工合成层中,产生的张力最小,并且在边坡趾部附近的土工合成层中产生的张力最大。 Shiwakoti等人也得出结论:在土工合成层中产生的张力分布非常不均匀,并且在边坡坡脚附近的加筋层中产生了最大张力。然而,这一假设与Zornberg和Arriaga进行的离心机研究相矛盾。他们总结称加筋层中最大峰值拉伸应变位于潜在滑动面与加筋层相交处,而这些峰值应变的最大值的位置(称为最大峰值拉伸应变)并不位于加固边坡趾部处的加筋层中,而是位于加固边坡大约中间高度的加筋层中。 Viswan adham和Mahajan进行的离心机研究也支持最大峰值张力位于中等高度位置的观点。最近杨等人进行了一项数值研究,并总结出峰值张力最大值的位置位于边坡中部附近。
假设峰值拉力分布将对设计产生重要影响,特别是当沿着加固边坡结构的高度采用不同的加固强度时。加固过程中峰值张力位置的错误假设可能会导致加筋层设计不当,从而导致边坡失稳。目前的研究调查了各种参数对最大张力的位置和大小,以及回填土中剪应变分布的影响。
问题描述
本文采用有限元软件PHASE2(Rocscience)对土工合成材料加筋土坡进行了参数研究,分析了剪应变分布中最大峰值张力的大小和位置在具有不同土和土工合成参数的边坡中的变化。以下参数是变化的,以研究它们对土工合成层中回填土中的剪切应变分布和张力移动的影响。
bull;土工合成材料的刚度(J)
bull;土工合成材料的垂直间距(s)
bull;顶部的加压压力(Q)
bull;坡度(beta;)
bull;回填土的摩擦角(ɸ)
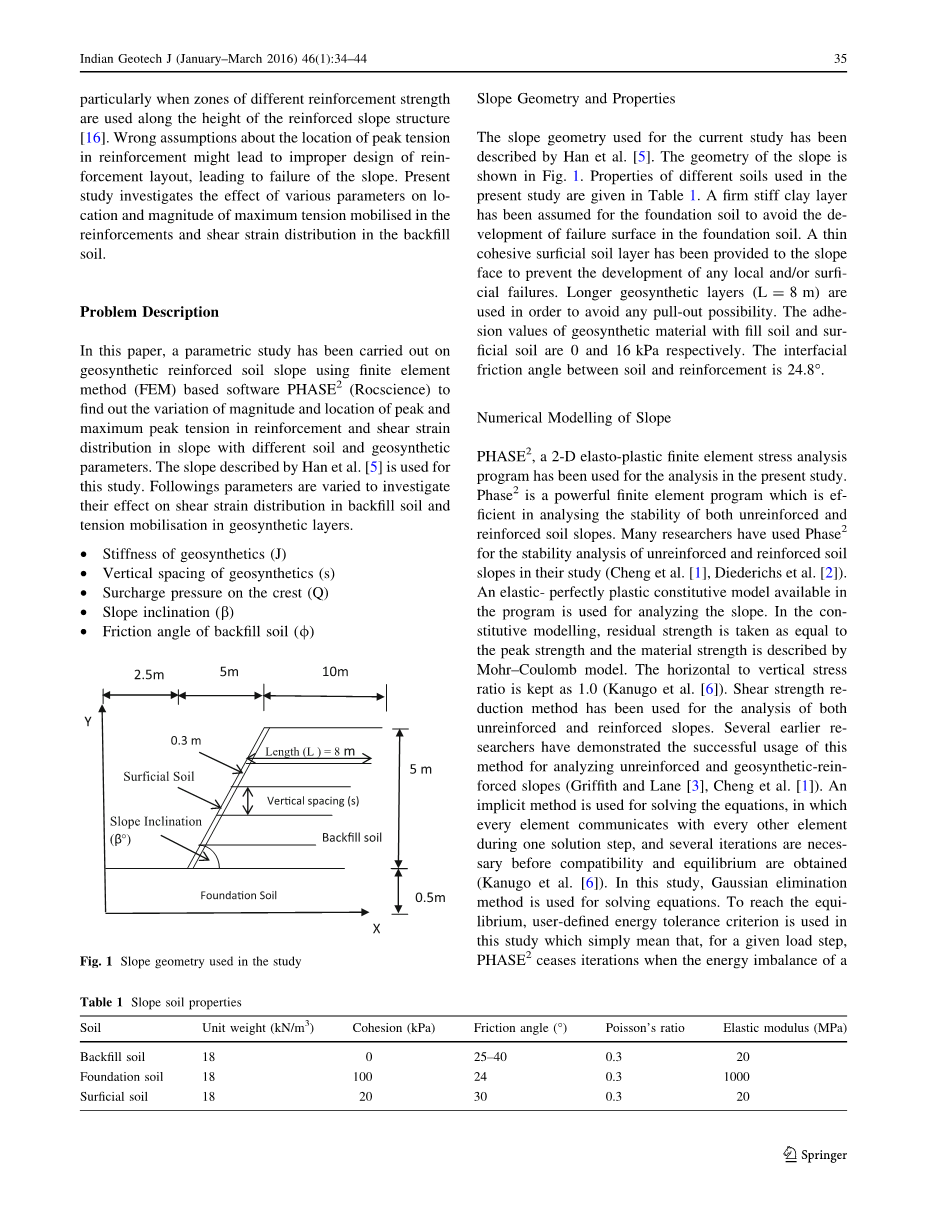
图1 边坡几何学在研究中的应用
表1边坡土性质
|
土类 |
容重(KN/M3) |
内聚力(KPA) |
摩擦角 |
泊松比 |
弹性模量(MPA) |
|
回填土 |
18 |
0 |
25-40 |
0.3 |
20 |
|
地基土 |
18 |
100 |
24 |
0.3 |
1000 |
|
表层土 |
18 |
20 |
30 |
0.3 |
20 |
边坡几何形状和属性
Han等人描述了当前研究中所用的边坡几何形状。边坡的几何形状如图1所示。表1中给出了本研究中使用的不同土的性质。为了防止地基土中的破坏面发展,假定地基土有坚硬的硬性粘土层。在坡面上提供了一个薄的粘性表层土,以防止任何局部和地表破坏的发展。 使用更长的土工合成层(L = 8米)以避免任何可能的破坏。填土和表层土的土工合成材料的黏附值分别为0和16 kPa。土与筋材之间的界面摩擦角为24.8°。
边坡数值模拟
本研究中使用了二维弹塑性有限元应力分析程序PHASE2。PHASE2可用于分析,它是一个功能强大的有限元程序,对无筋和加筋土边坡的稳定性分析是有效的。许多研究人员使用PHASE2程序在研究中对无筋和加筋土坡的稳定性进行了分析(程等人,Diederichs等)。程序中可用弹塑性本构模型进行边坡分析。在本构模型中,残余强度与峰值强度相等,材料强度可用Mohr-Coulomb模型描述。水平垂直应力比保持为1.0(Kanugo等)。剪切强度降低法已用于分析无筋和加筋边坡。早期的一些研究人员已经证明了这种方法可以成功地用于分析未加筋土工合成材料加筋边坡(Griffith和 Lane,程等人)。隐式方法用于求解方程,其中每个元素在一个求解步骤中与每个其他元素进行通信,在获得兼容性和平衡之前需要多次迭代(Kanugo等)。在这项研究中,高斯消除法用于求解方程。为了达到平衡,在本研究中使用用户定义的能量容差标准,这意味着,对于给定的负载阶跃,当前状态的能量不平衡状态达到初始能量不平衡状态的一小部分时,PHASE2停止迭代(能量不平衡 在第一次迭代)。 如果在指定的最大迭代次数内不满足此条件,结果将被视为未汇集(Kanugo等)。 对于目前的研究,使用0.1%的能量容差。
有限元离散化与网格划分
二维三节点三角平面应变元素已被用于离散化的边坡剖面,如图2所示。大约4000个元素被用来将斜率剖面离散化为具有大约2200个节点的均匀网格。 已经进行了详细的网格收敛研究,以获得与网格无关的解决方案。 据观察,当元素数量进一步增加时,安全系数值没有进一步的改善;,只有时间显著增加。这被称为h-收敛方法(Kanugo等)。 目前研究中的土工合成材料使用结构界面建模,允许在界面的两侧滑动。
图2 PHASE2(Rocscience)中制备的边坡的数值模型
安全因素的定义
这里定义的斜率的安全系数,是指原始剪切强度参数不足以使斜率达到失败边缘的因数。对于Mohr-Coulomb材料模型,因子抗剪强度参数cf和ɸf计算如下:
其中SRF是“强度折减系数(SRF)”。这种方法被称为“剪切强度折减(SSR)技术”(Matsui和Sam)。 PHASE2执行从SRF = 1开始的SRF值的系统搜索,这会导致边坡失稳。获得的最终值是安全系数(FOS)或SRF。
失败标准
在限制边坡中的应力或变形等可能的失效定义中,失效指标被视为非收敛性的结论(Zienkiewicz 和Taylor,Griffiths 和 Lane)。当FEM算法无法在用户指定的最大迭代次数范围内收敛时,其没有能够同时满足应力分布的Mohr-Coulomb破坏准则和全局平衡(Griffiths和Lane)。伴随着网格内节点位移的急剧增加,边坡失效和数值非收敛同时发生。在失效时,在所有元素处于塑性状态的边坡内形成一条破裂带,并且破裂带将从趾部穿过边坡到顶部(Kanugo等)。
初始模型验证
对于图1所示的几何结构分析模型,保持斜率(b)的倾角为45°。阶段2中模拟了非加固和加固的边坡模型。加筋边坡有四层土工合成筋,间距为1米。表1给出了地基土,表层土和回填土的性质。为了验证模型,回填土的摩擦角取为30°。假设筋材的拉伸强度为20 kN / m,筋材的拉伸刚度假定为1000 kN / m。这些属性来自Han等人的研究。比较和验证结果,本研究获得的非加固和加固情况的应力折减方法获得的安全系数(FOS)分别为0.91和1.5。由Han等人报道,由极限平衡法计算的 非加固和加固情况的安全因素分别为0.89和1.56。由Han等人报道,通过有限差分程序获得非加筋和加筋边坡的相应FOS,Continua的快速拉格朗日分析值(FLAC)分别为0.88和1.55。 图3比较了从本研究获得的未加固和加固边坡模型与Han等人获得的失效曲面。 对于相同的边坡模型采用极限平衡法。 从图3中可以看出,目前研究得到的未加筋和加筋边坡的潜在破坏面与Han等人获得的破坏面非常吻合。
然后将数值研究扩展到不同的加固边坡模型情况,改变边坡倾斜度,筋材间距和拉伸刚度,回填的摩擦角以及顶部的附加压力。表2给出了在各种数值模拟中变化的参数。 这个参数研究的结果在下一节讨论。
图3 潜在失稳面对照(a为未加固边坡,b为加固边坡)
结果与讨论
加固刚度的影响
在第一组参数研究中,筋材的拉伸刚度从100到4000 kN / m不等,如前面提到的(Han等人)对加筋边坡进行的数值研究。在这组研究中,其他所有参数都保持不变,如表2所示。比较了不同模型中筋材的拉力,并对不同的筋材刚度进行了比较。发现在具有低或中等拉伸刚度的土工合成层中动态张力最大(J =200-400 kN / m),如图4a所示。在特定的刚度(在这种情况下J = 800kN / m)下加固,发现加固刚度对张力移动的影响可以忽略不计。原因可以解释如下。当用刚度高达J = 800 kN / m的土工合成材料加固边坡时,边坡可视为欠加固,因此加固中的应力很高。但是,当土工合成刚度超过此值时,边坡过度加固,因此在达到恒定值之前,土工合成材料中的张力移动减少。所以可以得出结论:土工合成材料的刚度是边坡加固过程中边坡张拉动力的重要参数,但是其效果在过度加固的边坡上达到饱和。早先的研究人员对土工合成加筋路堤(Rowe和Li)和土工合成加固基础(Latha和Somwanshi)进行了类似的观察。从这组研究中可以得出结论,在边坡上不需要设置非常坚硬的土工合成材料,因为它们在产生一定的的影响后影响效果会变得很小。然而,在一些较早的研究中(Han等人)发现,张力在沿其长度方向上会更均匀地分布在更硬的土工合成材料中。因此,应根据张力移动的大小及其沿长度的分布来采用最佳的筋材刚度。
当比较不同拉伸刚度下的峰值加固张力与坡度的关系曲线时,最大峰值张力的位置位于边坡以上约2m处(边坡低于坡顶约60%),如图4a所示。这一观察结果与之前在土工合成材料加筋土坡上进行的一些离心机研究(Zorenberg和 Arriaga,Vishwanatham和Mahajan)非常吻合。在本研究中观察到的峰值张力的分布与三角形峰值张力分布的假设相矛盾,该假设认为在坡脚处出现最大峰值张力(Shiwakoti等)。 已发现最大峰值张力的位置与加固刚度一致,然而,最大峰值张力的幅度随着加固刚度的增加而减小,直至刚度值为800kN / m,之后其稳定。
表2 数值分析中的参数变化
|
组 |
J (kN/m) |
Tult (kN/m) |
S (m) |
ɸ (°) |
beta; (°) |
Q (kPa) |
|
1 |
100-4000 |
20 |
0.5 |
30 |
45 |
0 |
|
2 |
800 |
20 |
0.25-1.5 |
30 |
45 |
0 |
|
3 |
800 |
20 |
0.5 |
30 |
45 |
0-80 |
|
4 |
800 |
20 |
0.5 |
30 |
40-60 |
0 |
|
5 |
800 |
40 |
1 |
25-40 |
45 |
0 |
大写字母代表不同研究组中的参数
图4筋材刚度的影响。
a峰值张力随坡度的变化 b回填土中最大剪应变随加固刚度的变化
图4b显示了回填土中最大剪应变(MSS)的变化与筋材刚度的变化。最大剪切应变的大小是随着土工
全文共8549字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[12206],资料为PDF文档或Word文档,PDF文档可免费转换为Word


