英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
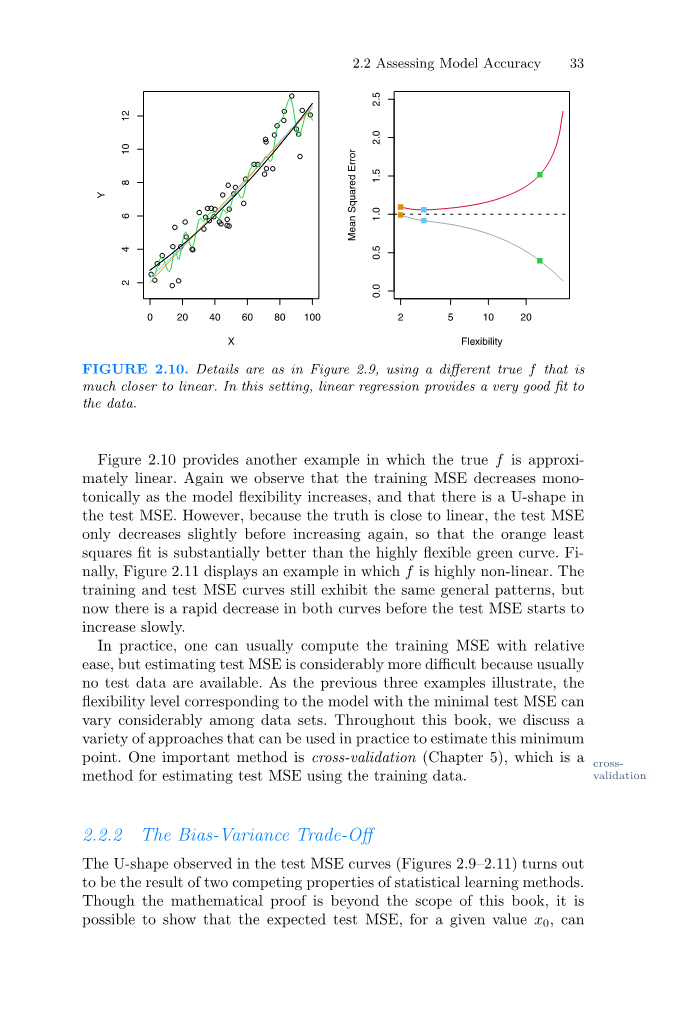
图2.10.细节如图2.9所示,使用另一个更接近于线性的真f。在这种情况下,线性回归为数据提供了一个非常好的拟合。
图2.10提供了另一个例子,其中真实的f几乎是线性的。我们再次观察到,随着灵活性模型的增加,训练的MSE在单调性上降低,在测试的MSE中存在一个U型。然而,由于真实情况接近线性,故检验MSE在再次增加之前略有下降,因此橙色最小二乘拟合明显优于高度灵活的绿色曲线。最后,图2.11显示了一个f高度非线性的例子。训练MSE曲线和测试MSE曲线仍然呈现出相同的一般规律,但是在测试MSE开始缓慢增长之前,两条曲线都出现了快速的下降。
在实践中,通常可以相对容易地计算出训练MSE,但是估计测试MSE要困难得多,因为通常没有测试数据可用。如前三个示例所示,在最小测试MSE的情况下,模型对应的灵活性级别在数据集之间可以有很大的差异。一种重要的方法是交叉验证(第五章),它是一种利用训练数据测试MSE的方法。
2.2.2偏方差权衡
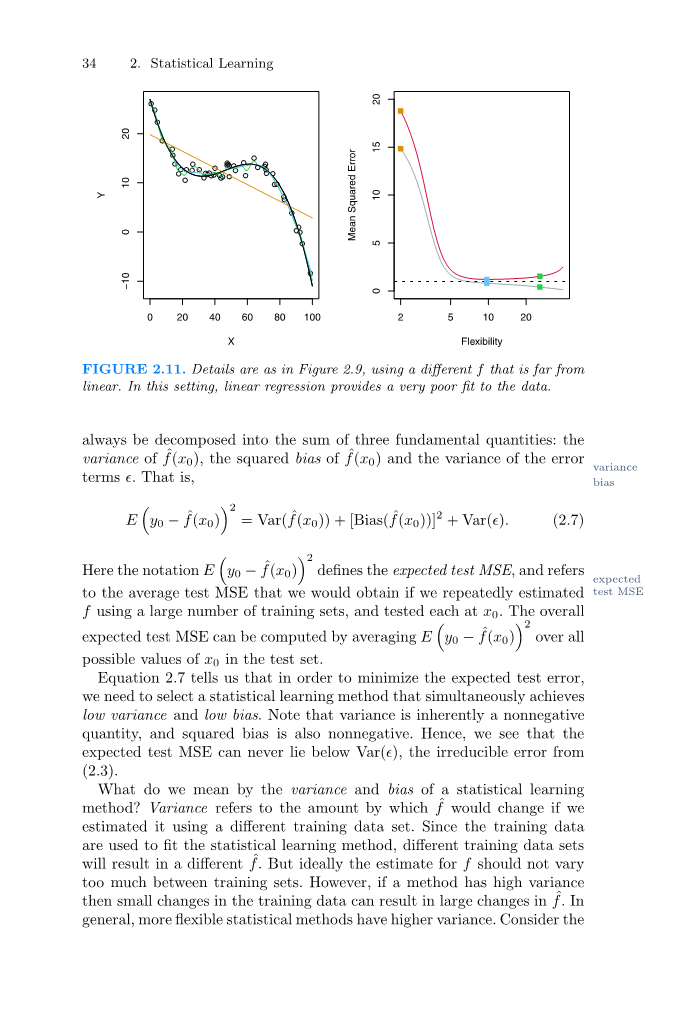
从U型中可以观察到测试MSE曲线(图2.9-2.11)是两个统计学习方法相互竞争的结果。虽然数学证明超出了本书的范围,但是可以显示预期的测试MSE,对于一个给定的值x0,总是能够分解为三个基本量的和:f(x0)的方差、f(x0)的平方偏差和误差方差项的方差。即
这里的符号E(y0-f(x0))2定义了预期的测试MSE,如果我们使用大量的训练集反复估计测试f,并且在x0上测试每个训练集,我们就有期望能得到平均测试MSE。总体期望测试MSE可以通过将E(y0-f(x0))2与测试集中所有可能的x0值来平均计算。
图2.11.细节如图2.9所示,使用不同的f,它不是线性的。在这种情况下,线性回归数据的拟合非常差。
等式2.7告诉我们,为了最小化预期的测试误差,我们需要选择一种同时实现低方差和低偏差的统计学习方法。请注意,方差本质上是非负的,平方偏差也是非负的。因此,我们看到预期的测试MSE永远不会低于Var (),来自( 2.3 )的不可约误差。
统计学习方法的差异和偏差是什么意思?方差是指如果我们使用不同的训练数据集来估计,f会改变的量。由于训练数据被用来适应统计学习方法,不同的训练数据集会产生不同的f值。但是理想情况下,f值在不同的训练集之间不应该变化太大。然而,如果一种方法具有高方差,那么训练数据的小变化会导致f的大变化。通常,更灵活的统计方法具有更高的方差。考虑如图2.9所示的绿色和橙色曲线。灵活的绿色曲线非常接近观察结果。它具有很高的方差,因为改变这些数据点中的任何一个都可能导致估计值发生很大变化。相比之下,橙色最小二乘直线相对不灵活,并且具有低方差,因为移动任何单个观测值都可能导致直线位置的微小偏移。
另一方面,偏差是指通过一个简单得多的模型来近似现实生活中的一个可能非常复杂的问题而引入的误差。例如,线性回归假设Y和X1、X2,...,Xp。任何现实生活中的问题都不太可能真的有如此简单的线性关系,因此执行线性回归无疑会导致f估计值的一些偏差。在图2.11中,真实的f基本上是非线性的,所以不管我们得到多少训练观测值,都不可能使用线性回归产生准确的估计值。换句话说,在这个例子中,线性回归导致高偏差。然而,在图2.10中,真实的f非常接近线性,因此给定足够的数据,线性回归应该有可能产生精确的估计。通常,更灵活的方法导致更少的偏差。
一般来说,当我们使用更灵活的方法时,方差会增加,偏差会减少。这两个量的相对变化率决定了测试MSE是增加还是减少。当我们增加一类方法的灵活性时,偏差最初会比方差增加更快地减少。因此,预期的测试MSE下降。然而,在某个时候,增加灵活性对偏差影响不大,但开始显著增加差异。当这种情况发生时,测试MSE会增加。请注意,我们在图2.9 - 2.11的右侧面板中观察到测试均方误差随后增加的模式。
图2.12中的三幅图说明了图2.9 - 2.11中示例的等式2.7。在每种情况下,蓝色实线代表不同灵活性水平的平方偏差,而橙色曲线代表方差。水平虚线表示Var (),不可约错误。最后,对应于测试集MSE的红色曲线是这三个量的总和。在这三种情况下,随着方法灵活性的增加,方差增加,偏差减少。然而,对应于最佳测试MSE的灵活性水平在三个数据集之间有很大差异,因为每个数据集的平方偏差和方差以不同的速率变化。在图2.12的左侧面板中,偏差最初迅速减小,导致预期测试MSE的初始急剧减小。另一方面,在图2.12的中央面板中,真实的f接近线性,因此随着柔性的增加,偏差只有很小的减少,并且测试MSE在随着方差的增加而快速增加之前仅略微下降。最后,在图2.12的右侧面板中,随着灵活性的增加,偏差急剧下降,因为真F是非常非线性的。随着灵活性的增加,差异也几乎没有增加。因此,随着模型灵活性的增加,测试MSE在经历小幅增加之前大幅下降。
图2.12.平方偏差(蓝色曲线)、方差(橙色曲线)、Var () (虚线),并测试图2.9 - 2.11中三个数据集的MSE (红色曲线)。垂直虚线表示对应于最小测试MSE的灵活性水平。
在等式2.7中给出并在图2.12中显示的偏差、方差和测试集MSE之间的关系称为偏差-方差权衡。统计学习方法的良好测试集性能需要低方差和低平方偏差。这被称为权衡取舍,因为很容易获得具有极低偏差但高偏差的方法(例如,通过绘制通过每一次训练观察的曲线),或者具有极低偏差但高偏差的方法(通过对数据拟合水平线)。挑战在于找到一种方差和平方偏差都很低的方法。这种权衡是本书最重要的重复主题之一。
在无法观察到f的真实情况下,通常不可能显式计算统计学习方法的测试MSE、偏差或方差。然而,我们应该始终牢记偏差-差异的权衡。在这本书中,我们探索了非常灵活的方法,因此基本上可以消除偏见。然而,这并不保证它们会比线性回归等简单得多的方法表现更好。举一个极端的例子,假设真f是线性的。在这种情况下,线性回归不会有偏差,这使得更灵活的方法很难竞争。相反,如果真f是高度非线性的,并且我们有大量的训练观察,那么我们可以使用高度灵活的方法做得更好,如图2.11所示。在第五章中,我们讨论了交叉验证,这是一种利用训练数据估计测试MSE的方法。
2.2.3分类设置
到目前为止,我们对模型精度的讨论一直集中在后悔设置上。但是,我们遇到的许多概念,例如偏差-方差权衡,由于yi不再是数字的,只需要一些修改就转移到分类设置。假设我们试图根据训练观测值{(x1,y1 )来估计f,...,( xn,yn)},其中现在y1,...,yn都是定性的。量化我们估计的准确性的最常见方法是训练错误率,即如果我们应用错误率,所犯错误的比例。我们对训练观察的估计:
这里lsquo;yirsquo;是使用lsquo;frsquo;进行第一次观察的预测类标签。I ( yi ne;ˇ yi )是一个指示变量,如果yi ne;ˇyi,则等于1,如果yi =ˇyi,则等于0。指示器如果I ( yi ne;ˇyi ) = 0,那么通过我们的变量分类方法,第i次观察被正确分类;否则它会被错误分类。因此,等式2.8计算不正确分类的分数。
等式2.8被称为训练错误率,因为它是基于用来训练分类器的数据而计算的。与误差回归设置一样,我们最感兴趣的是将分类器应用于测试训练中未使用的观测结果所产生的误差率。与表单测试误差( x0,y0)的一组测试观测值相关联的测试误差率由下式给出保存
其中,ˇy0是通过将分类器应用于具有预测器x0的测试观察而得到的预测类标签。一个好的分类器是测试误差( 2.9 )最小的分类器。
贝叶斯分类器
有可能表明(尽管证据不在本书的范围内),平均来说,( 2.9 )中给出的测试错误率通过一个非常简单的分类器被最小化,该分类器根据预测值将每个观察值分配给最可能的类。换句话说,我们应该简单地将带有预测向量x0的测试观测值分配给j类,其
是最大的。请注意,(2.10)是条件概率:给定观察到的预测向量x0,Y = j是条件概率。这种非常简单的类概率分类器被称为贝叶斯分类器。在两类问题中,贝叶斯分类器只有两个可能的响应值,比如类别1或类别2,如果Pr(Y = 1|X = x0) gt; 0.5,则对应于预测第一类,否则对应于预测第二类。
图2.13.一个模拟数据集,由两组中的每组100个观察数据组成,用蓝色和橙色表示。紫色虚线表示贝叶斯决策边界。橙色背景网格表示测试观察将被分配给橙色类别的区域,蓝色背景网格表示测试观察将被分配给蓝色类别的区域。
图2.13提供了一个在由预测因子X1和X2组成的二维空间中使用模拟数据集的例子。橙色和蓝色圆圈对应于属于两个不同类别的训练观察。对于X1和X2的每个值,响应为橙色或蓝色的概率不同。由于这是模拟数据,我们知道数据是如何生成的,我们可以计算X1和X2的每个值的条件概率。橙色阴影区域反映Pr(Y =橙色|X )大于50 %的点集,而蓝色阴影区域表示概率低于50 %的点集。紫色虚线表示概率正好为50 %的点。这被称为贝叶斯决策边界。贝叶斯判别边界分类器的预测由贝叶斯决策边界决定;落在边界橙色侧的观察将被分配给橙色类,类似地,边界蓝色侧的观察将被分配给蓝色类。
贝叶斯分类器产生尽可能低的测试错误率,称为Bayes错误率。由于Bayes分类器总是选择类别Bayes误差( 2.10 )最大的类别,因此X = x0时的误差率为1 – Maxj Pr ( Y =速率j|X = x0 )。一般来说,总体贝叶斯错误率由下式给出
其中期望值平均了X的所有可能值的概率。对于我们的模拟数据,Bayes错误率是0.1304。它大于零,因为类在真实总体中重叠,所以对于x0的一些值,最大值Pr(Y = j|X = x0) lt; 1。Bayes误差率类似于前面讨论的不可约误差。
K-最近邻
理论上,我们总是希望使用贝叶斯分类器来预测定性反应。但是对于真实数据,我们不知道给定X的Y的条件分布,因此计算Bayes分类器是不可能的。因此,Bayes分类器是一个不可企及的黄金标准,可以用来比较其他方法。许多方法试图估计Y给定X的条件分布,然后将给定观测值分类到具有最高估计概率的类别。一种这样的方法是K -最近邻( KNN )分类器。给定一个正的- K -最近的teger K和一个测试观察值x0,KNN分类器首先识别训练数据中最接近x0的邻居K点,由N0表示。然后,它将j类的条件概率估计为N0中响应值等于j的点的分数:
最后,KNN应用贝叶斯规则,将测试观测值x0分类到概率最大的类别。
图2.14提供了KNN方法的一个示例。在左侧面板中,我们绘制了一个由六个蓝色和六个橙色观察组成的小训练数据集。我们的目标是预测黑色十字标记的点。假设我们选择K = 3。然后KNN将首先识别最接近十字架的三个观察点。这个邻域显示为一个圆圈。它由两个蓝色点和一个橙色点组成,导致蓝色类的估计概率为2 / 3,橙色类的估计概率为1 / 3。因此KNN会预测黑色十字属于蓝色类。在图2.14的右侧面板中,我们已经在X1和X2的所有可能值上应用了K = 3的KNN方法,并在相应的KNN决策边界中绘制。
尽管这是一种非常简单的方法,KNN通常能够产生出令人惊讶地接近最佳Bayes分类器的分类器。图2.15显示了当应用于图2.13中较大的模拟数据集时,使用K = 10的KNN决策边界。请注意,即使KNN分类器不知道真实的分布,KNN决策边界也非常接近Bayes分类器的边界。使用KNN的测试错误率为0.1363,接近Bayes错误率0.1304。
图2.14.使用K = 3的KNN方法在一个简单的情况下进行了说明,有六次蓝色观察和六次橙色观察。左:需要预测类标签的测试结果显示为黑色十字。识别与测试观察最接近的三个点,并且预测测试观察属于最常见的类别,在这种情况下是蓝色的。右:此示例的KNN决策边界以黑色显示。蓝色网格表示测试观察将被分配给蓝色类的区域,橙色网格表示测试观察将被分配给橙色类的区域。
K的选择对所获得的KNN分类器有很大的影响。图2.16显示了两个KNN拟合图2.13中的模拟数据,使用K = 1和K = 100。当K = 1时,决策边界过于灵活,会在数据中发现不符合Bayes决策边界的模式。这对应于具有低偏差但方差非常高的分类器。随着K的增长,该方法变得不那么灵活,并产生接近线性的决策边界。这对应于低方差但高偏差的分类器。在这个模拟数据集上,K = 1或K = 100都不能给出好的预测:它们的测试误差率分别为0.1695和0.1925。
正如在回归设置中一样,训练错误率和测试错误率之间没有很强的关系。K = 1时,KNN训练错误率为0,但测试错误率可能相当高。通常,随着我们使用更灵活的分类方法,训练错误率会下降,但测试错误率可能不会下降。在图2.17中,我们绘制了KNN测试和训练误差作为1/K的函数。随着1/K的增加,该方法变得更加灵活。与回归设置一样,随着灵活性的增加,训练错误率
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[426653],资料为PDF文档或Word文档,PDF文档可免费转换为Word


