
英语原文共 9 页,剩余内容已隐藏,支付完成后下载完整资料
单位范数约束线性拟合问题的快速稳健估计
Daiki Ikami Toshihiko Yamasaki Kiyoharu Aizawa
日本东京大学
{ikami, yamasaki, aizawa}@hal.t.u-tokyo.ac.jp
摘要
采用迭代重加权最小二乘(IRLS)的M-估计是最著名的鲁棒估计方法之一。然而,对于鲁棒单位范数约束线性拟合(UCLF)问题,IRLS是无效的,例如基本矩阵估计,因为初始解很差。我们通过开发一个新的目标函数及其优化来克服这个问题,命名为迭代重加权特征值最小化(IREM)。IREM保证了目标函数的减少,收敛速度快,鲁棒性强。在鲁棒基本矩阵估计中,IREM的执行速度比随机抽样一致性(RANSAC)快5-500倍,同时保持可比较的或更好的鲁棒性。
- 介绍
单位范数约束线性拟合(UCLF)问题的鲁棒估计可以表述为:
(1)
其中p(r)是一个鲁棒损失函数。这种公式常用于圆锥曲线估计[24]和基本矩阵估计[11]等情况。
采用迭代重加权最小二乘(IRLS)算法[12]的m估计是鲁棒线性回归中最常用的技术之一。尽管我们可以将这种技术用于鲁棒UCLF问题,它仍然是无效的,因为作为IRLS的初始解的最小二乘(LS)解很差。
我们将演示为什么初始LS解对于UCLF问题是如此糟糕的解决方案。考虑到鲁棒平面拟合问题,它可以表示为方程(1)1,LS的平面拟合结果如图1所示。图1(d)中的LS解离鲁棒估计的解太远了。另外,UCLF是一个具有多个局部极小的非凸优化问题;因此,从一个糟糕的初始解出发的现有的的迭代解法,经常会陷入局部极小值不足的问题中。
(a) 时的点分布 (b)时的点分布
(c) 图1(a)加一个孤立点后 图(d) 图1(b)加一个孤立点后
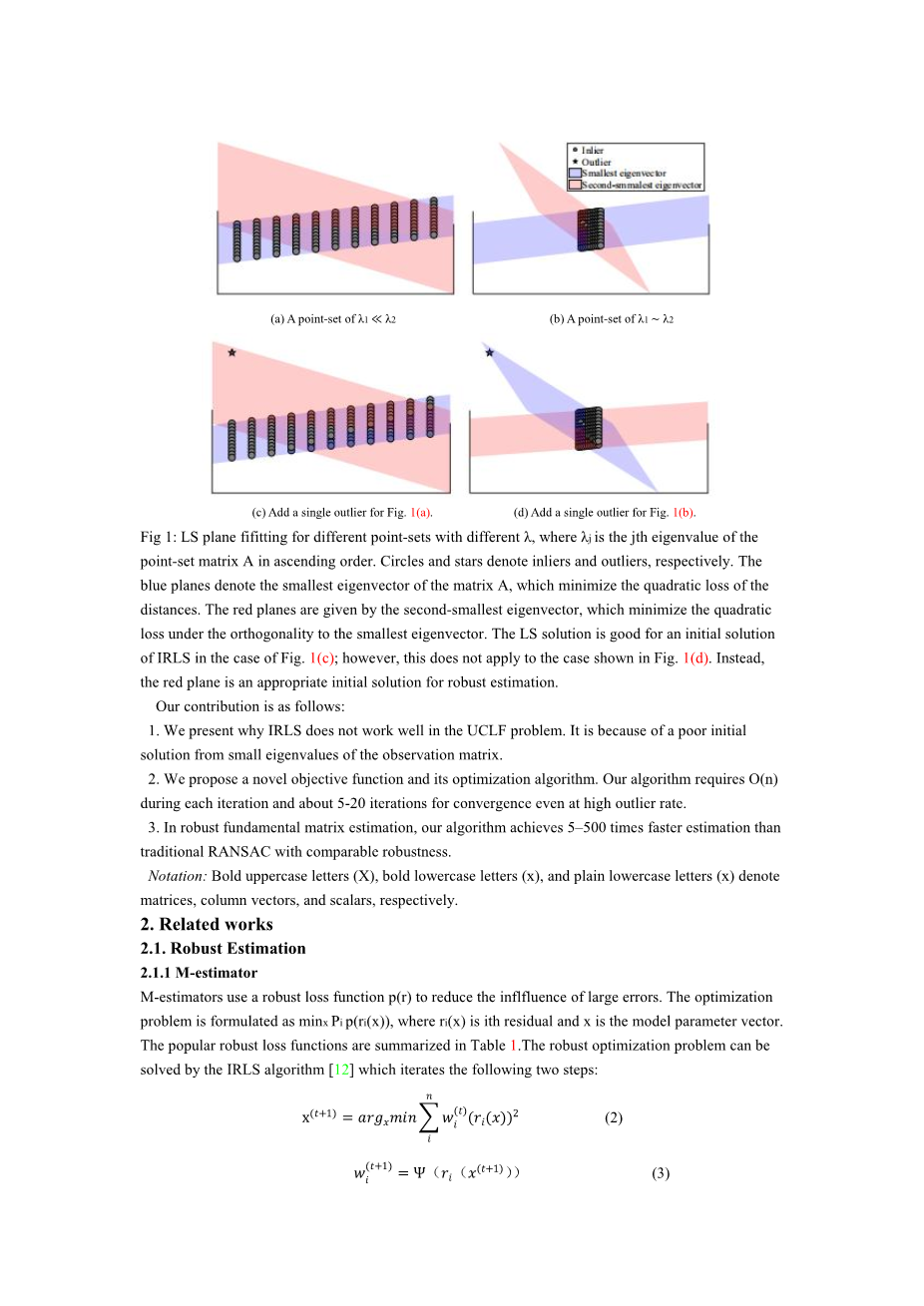
图1:lambda;取值不同时,不同点集的LS平面拟合,其中是点集矩阵A在升序排列中的第j个特征值。圆形和星形分别表示内点和外点。蓝色平面表示矩阵A的最小特征向量,它们最大限度地减少距离的二次损失。红色平面由第二小特征向量给出,它们把正交状态下最小特征向量的二次损失降到最低。在图1(c)的情况下,LS解适用于IRLS的初始解;然而,这不适用于图1(d)所示的情况。相反,红色平面是鲁棒估计的一个合适的初始解。
在本研究中,我们通过利用一个隐藏的良好初始解的方法提出了一种新的M-估计的近似目标函数,克服了初始解不足的问题,如图1(D)中的红色平面所示。我们的近似目标函数可以通过一种名为迭代重加权特征值最小化(IREM)的收敛性保证的算法来实现最小化。因为最优化问题的非凸性,导致IREM不一定能找到全局最优解。然而,实验评价的结果表明,IREM即使在40-70%的异常率较高的情况下也能找到一个很好的解决方案。在每次迭代中,IREM只需要计算O(n),其中n是观测数据点的总数,需要5-20次迭代才能达到收敛。
我们的贡献如下:
1. 展示了为什么IRLS在UCLF问题中不能很好地工作。这是因为观测矩阵的小特征值的初始解很差。
2. 提出了一种新的目标函数及其优化算法。我们的算法在每次迭代中都需要O(n),即使在较高的离群率下也需要5-20次迭代才能收敛。
3. 在鲁棒基本矩阵估计方面,我们的算法的估计速度比传统的RANSAC算法快5-500倍,同时具有更好的鲁棒性。
符号:粗体大写字母(X)、粗体小写字母(x)和普通小写字母(x)分别表示矩阵、列向量和标量。
2 相关工作
2.1 鲁棒估计
2.1.1 M估计
M-估计器使用鲁棒损失函数p(r)来减小大误差的影响。将优化问题表述为,其中为第i次残差,x为模型参数向量。表1总结了常用的鲁棒损失函数。
表1:代表方程(3)和方程(4)中的损失函数p(r)及其响应函数psi;(r)
|
最小绝对值 |
Huber |
Cauchy |
Talwar |
|
|
p(r) |
||||
|
psi;(r) |
1 |
|
||
|
F(w) |
鲁棒优化问题可以用迭代以下两个步骤的IRLS算法[12]来求解:
(2)
(3)
其中psi;(r)是从p(r)导出的权函数,如表1所示。IRLS迭代方程(2)和方程(3)直到收敛。请注意,IRLS是一种优化-最小化[13]。我们可以用加权最小二乘法[2,23,27]构造p(r)的一个优化函数:
(4)
其中是第i个基准的权重,f(w)是从p(r)导出的函数,如表1所示。注意,在方程(4)中IRLS等价于交替优化策略。以塔尔瓦损失为例,基于方程(4)的优化问题是
(5)
通过方程(5)解得为
(6)
从方程(6)我们可以发现方程(5)等价于Talwar损失最小化问题,以及方程(5)的交替极小化等价于IRLS,正如在方程(3)一样。
2.1.2 随机抽样一致性算法
RANSAC[10]是目前最流行的基于随机优化的鲁棒估计方法之一。RANSAC有两个步骤:模型参数的假设是由从观察数据集中随机选择的极小样本子集构造而来的。然后从所有观测数据中计算出该假设的得分。RANSAC迭代这个过程,直到找到一个分数足够的模型参数。
RANSAC的计算量随离群率和参数维数的增加而增加。设w是变量的比例,d是参数的维数。我们可以选择一个样本集的所有不动点的概率为。因此,我们可以在试验n中选择一个概率为的全差集,并得到以下公式:
(7)
方程(7)指出RANSAC需要n次迭代才能在置信度p处进行正确估计。因此,RANSAC在高离群率和大参数维数的情况下需要大量的计算量。
RANSAC有各种扩展,例如各种评分函数[17,22]和利用相似分数[7]。Raguram以及其他人介绍了一种复杂的方法USAC[16],比如SPRT测试[8]和局部优化[9]。
2.2 风险矩阵估计
尽管我们的方法可以应用于任何鲁棒的UCLF问题, 但本文主要研究的是鲁棒基本矩阵估计,这是计算机视觉应用中的一项重要任务,例如立体声问题和三维重建。基本矩阵估计一般有三个步骤:(1)通过提取和匹配特征点获得相应的点(包括异常点);(2)采用鲁棒估计技术消除异常值;(3)从正确的对应点估计基本矩阵。虽然第三步中,如对基本矩阵估计施加极约束和秩-2约束[20,25,4,26],是一个重要的研究领域,但我们的研究集中在第二步:异常点拒绝。
基本矩阵是从通过局部特征匹配进行提取的相应的点来进行估计的。给定两个像之间的对应点和,基本矩阵F满足极约束:
(8)
从极约束出发,我们可以通过求解以下LS问题来估计基本矩阵:
(9)
其中是n个正确对应的矩阵。这就是众所周知的八点算法[14,11]。方程(9)可以用奇异值分解(SVD)得到的A的最小特征向量来求解。注意方程(9)是一个非凸优化问题,因为解集被限制在一个非凸集的球面上。
将鲁棒基本矩阵估计定义为方程(1), 它使用鲁棒损失函数代替方程(9)中的二次函数。在最小估计的IRLS算法中,采用LS解作为初始猜测。然而,由于优化问题的初始解差和非凸性,IRLS往往无法准确地估计参数。据报道,初始LS解的IRLS收敛到10%到15%的离群点[19,21]的局部极小值。
用RANSAC[10]等概率方法可以避免初始解问题,这种方法不需要初始解。这些方法在速度和鲁棒性方面是实用的,但它们的问题很大,因为它们极大地增加了计算成本,而且异常值的频率很高,如2.1.2节所述。
最近,程以及其他人[5]提出了一种新的基于秩-2约束的鲁棒优化方法。虽然他们的方法得到了鲁棒估计,但因为需要解决半定规划问题,这种方法需要相当长的处理时间。
3. 初步工作:鲁棒UCLF问题
在描述我们的方法之前,我们引入了最小特征值最小化问题,它等价于方程(1)中的鲁棒UCLF问题。然后,如图1所示,我们给出了初始LS解问题不佳的原因。
3.1 最小特征值极小化问题
在这一部分中,我们证明了鲁棒UCLF问题可以转化为一个最小特征值最小化问题。通过使用剩余项和方程(4),方程(1)的鲁棒UCLF问题可转化为
(10)
其中是对角矩阵。
就像解方程(9)一样,方程(10)的优化问题可以用来解出x,其中是按升序排序的的第i个特征向量。从,其中是矩阵的第i个特征向量,方程(10)可转化为以下等价优化问题:
(11)
因此,鲁棒UCLF问题方程(10)等价于w上最小特征值极小化问题。
3.2 鲁棒UCLF中的差初始解
在本节中,我们解释了为什么LS解在鲁棒UCLF问题中往往是一个差的初始解,如图1(d)所示。设不存在孤立点和独立点噪声,即,并且和分别是的第j个特征值和特征向量。注意,对于所有i,有,而是A的LS解。
我们考虑矩阵的一个LS解,其中,是孤立点,即。解x可以写成的线性组合:,其中。从,可以得到
(12)
我们用约束条件把方程(12)化简后来表示c:
(13)
其中和z是满足的归一化项。如果对所有的,有,即是矩阵的近LS解。但是,如果存在j,使得,则是矩阵近LS解,如图1(D)所示。
4. 推荐方法
在这一部分中,我们提出了一个特征值极小化问题,它是方程(11)的一个近似问题,并且是一种最小化目标函数的算法。
4.1 初步观察
如第3.2节所述,LS解,最小特征向量,可能不适合于鲁棒UCLF问题的初始解。我们发现,在这种情况下,其他的特征向量似乎有助于鲁棒估计。图2(b)-(j)表示基矩阵估计中每个特征向量计算的残差。虽然我们不能从最小特征向量中判断第二次对应值是一个离群点,但我们可以从第三小特征向量判断。在此基础上,我们提出了一种利用多特征向量避免初始解差的方法。
4.2问题公式化
我们提出了方程(11)的一个近似方程,如下:
(14)
为了简化表示,被写成。
接下来我们将解释这种近似的理由。假设内点不包含噪声,并使用硬阈值损失函数(例如Talwar损失)。如果第i次观察是一个内点,则。如果第i次观测是一个离群点,当w接近解时则有。因此,保留。如有方程(11)对x有唯一的解,那么对,有。因此,和是满足的,并且方程(14)的第一项可等价为
(15)
因此,当w接近最优解时,我们的近似方程(14)接近原目标函数方程(11)。
这种近似有很好的性质:(1)方程(14)是一个k特征值最小化问题,它不仅可以利用最小的特征向量,而且还可以利用其他特征向量,如图1(D)中的第二最小特征向量;(2)它具有快速收敛性。
4.3 优化
我们描述了方程(14)的优化方法。我们的优化是基于优化最小化,它确保了减少(或不变)原来的目标函数。首先,使用Jensen不等式将优
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[448295],资料为PDF文档或Word文档,PDF文档可免费转换为Word


