
英语原文共 22 页
非稳定重力流水力学
虽然大多数收集系统的设计都是基于稳定流水力学,但污水管道中的水流基本上是不稳定的。由于以下原因:
- 家庭和工业日用水量的变化导致的流量不稳定
- 在潮湿天气时水流入和渗入导致的变化
- 水泵的循环开闭
- 流量调节装置的性能
- 湿井下游水位变化
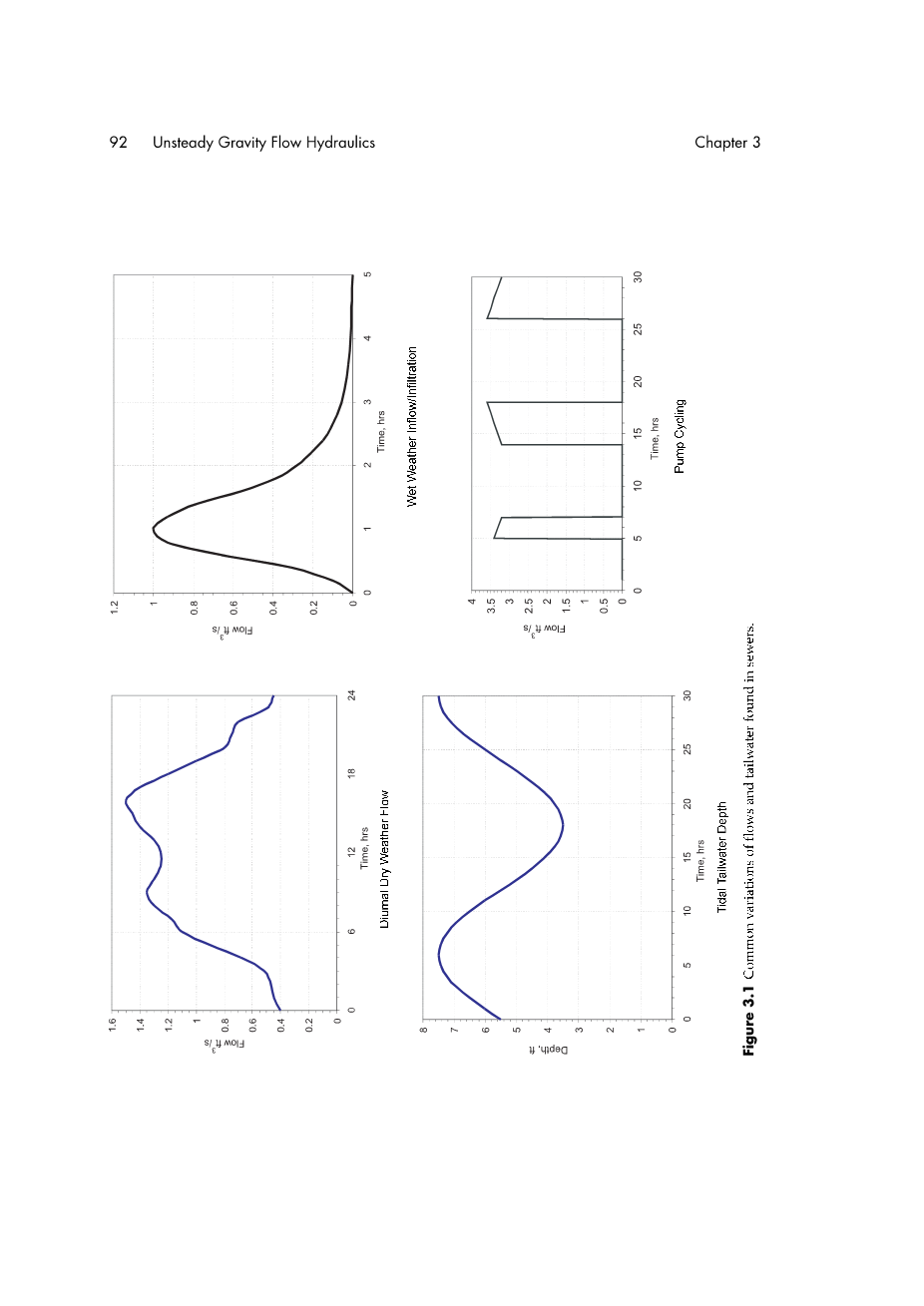
这些随时间变化的条件如图3.1所示。在分析现有下水道系统的容量限制和水流溢出时尤其重要。与为新土地开发设计污水渠的问题不同,在旧系统中,非稳定水流和溢流已成为关键问题。对泵站的分析还需要对流量的时间变化进行量化。
水流在收集系统中逐渐移动时也会变化。随着管道上游端流量的增加,水位和流速也随之增加,进而向下游移动。此外,流动状态也可能发生变化。在面对暴雨时,组合下水道中的水流一开始是部分满的,但可能会变成满流,然后随着下游水在顺游时流量的增加而受压,从而限制了水的流量。
图 3.1 下水道中的流量和尾水的常见变化
非稳定流流动分析的基础知识是通过下水道系统对非稳定流流动进行建模,称为流动路径。国家工程手册(美国土壤保持局,1972年)将路线定义为“从上游点计算到下游点的洪水量,考虑储存。”随着稳定流量的干扰向下游移动,峰值由于一些水在称为衰减的过程中增加深度,因此干扰趋于平缓。
在稳定流动中,深度和流速之间存在独特的关系(即,正常深度,水面平行于通道底部)。这种关系称为评级曲线。然而,对于不稳定的流动,深度偏离正常深度。在增加(上升)流动期间水面的斜率大于通道底部斜率并且在减小(下降)流动期间比通道底部斜面更平坦。这导致循环评级曲线,如图3.2所示。
图 3.2 环状阶段 - 放电曲线的例子
有许多方法可以解决收集系统中的不稳定流动,从理论上完整的St. Venant方程(第3.3节)到简单的水逻辑路由方法(在后面的章节中描述)。用于确定下水道流量的方法已经从为解决溪流中的洪水问题而开发的方法发展而来。然而,由于潜力,它们相当复杂。下水道在全管加压流和干燥之间运输。
本章的其余部分描述了用于解决非稳态流问题的方程以及这些方程在实际采集系统中的应用。
路由类型
液压模型通过系统跟踪流量和液压等级,而水文模型跟踪流量并使用简化的近似来计算动量效应。水文路线方法也称为集总模型,因为它们计算到达范围的一个位置(下游端)的流量。 Hydrau-lic路由模型被称为分布式模型,因为它们同时计算几个横截面的流量(Fread,1993)。
管道中流动的衰减是由于每个管道范围内的临时存储造成的。 Hydrau-lic方法在确定存储的体积时明确考虑了水的深度。在许多情况下,管道的几何形状非常复杂,以至于确定存储所需的工作量过大,因此存储通过简化的存储方程来近似。水文方法假设知道在当前和之前的时间步骤期间的流入以及在前一时间步骤期间的流出足以阻止从到达的流出。一旦知道了流入和流出,如果需要,可以使用逐渐变化的流动方法或甚至正常深度来确定水深。
水文路由方法依赖于存储方程:
其中1 =流入(ft3/ s,m3 / s)
Q =流出(ft3 / s,m3 / s)
s =存储(ft3,m3)
已开发出各种方法用于计算流入量的流量或管道流量的流出量。如果下游条件不支持流量,这些方法通常是准确的;也就是说,如果尾水深度和流量限制不会显着降低下游流量。当存在下游限制时,水文路线方法倾向于预测高于水力模型的峰值并且更早到达,因为它们没有充分考虑导致衰减的所有因素。
流体力学方程
用于模拟下水道中非定常流动的最常用方程基于以下假设:流动是一维的,压力分布是流体静力学的,通道的长度远大于深度,并且水密度是恒定的。在这种条件下,流体中的扰动被称为shalow-uwater或franslatory wave(Linsley,Kohler和Paulhus,1982)。Saint-Venant方程下水道中的一维流动最好用Jean-Claude Barre de St. Venant的方程来描述。它们是三维Navier-Stokes方程的简化。)它们基于这样的假设:横截面中的平均速度足以描述流动,而水面仅在流动方向上倾斜。 Saint-Venant方程由两个偏微分方程组成 - 一个用于连续性,另一个用于动量 - 并且具有许多不同的形式。 French(1985)给出了连续性方程:
而动量方程为
其中a =纵向速度(ft / s,m / s)
x =纵向距离(ft,m)
y =水深(m,ft)
g =重力加速度(32.2 ft / s2,9.81 m) / s2)
So =通道床在纵向上的斜率(ft / ft,m / m)
S =摩擦斜率(ft / ft,m / m)
求解这些方程所需的初始和边界条件。边界条件通常是出口处的流入水文和尾水条件,并且初始条件是基于分析开始时的某些预定流量逐渐变化的流动剖面(或正常深度)。
Saint-Venant方程不能通过分析求解,因此已经开发了各种数值解。这些方法可以分为有限差分方法或特征方法。而特征方法适用于突发突发波对于下水道系统中遇到的流量变化类型,优选有限差分方法。
Finitedifference解决方案将空间和时间划分为一个网格,如图3.3所示,并将近似导数作为有限差分,如
有很多文章描述了解决这些方程的方法,包括Abbott,1979; Chow,1973; Cunge,Holley和Verwey,1980; Fread,1993; French,1985; NOAA,2000; Ponce,Li和Simons,1978; Price,1973; Roesner,Aldrichson,1989; Yen,1996; and Yen,2001.所有都涉及关于是否应使用隐式或显式方法的讨论。显式解决方案更容易编程,但隐式解决方案往往更稳定。数值解中使用的点数也会影响收敛性和准确性。
特别是,明确的方法需要很小的时间步长(在潮湿天气条件下大约10秒)(Roesner,Aldrich和Dickinson,1989)。数值稳定性问题可以表现为流动和表面高度的振荡,过度的速度或连续性误差。时间步长应基于表面波在管道长度上移动所需的时间,该近似值为
其中△t=波浪行进的时间管道的长度
L =管道的长度(ft,m)
g=重力加速度(32.2 ft / s2,9.81 m / s2)
D =管道的直径(ft,m)
有限差分方程的成功解决方案取决于时间和距离步长的选择。较大的步长会导致更快的解决方案,但更容易出现不稳定和不精确。有许多计算机程序可供使用,因此通常不会对下水道中的不稳定流动进行人工计算。
图 3.3 有限差分网格
流体力学方程的逼近
由于难以求解Saint-Venant方程,因此已经开发了许多近似值。大多数涉及从动量方程中消除项以提高稳定性。可以重新排列和简化St. Venant动量方程,以找出作为正常流量下的流量和动量方程中的项的函数的放电(Weinmann和Laurenson,1979; French,1985)。
其中Q =实际非定常流量(ft3 / s,m3 / s)
QN=正常条件下的流量(t3 / s,m3 / s)
当考虑括号中的所有项时,则方程3.6对应于Saint-Venant方程。当括号中的最后一项被忽略时,模型被称为扩散类比,并且流动不会突然改变,如在上游的泵循环中。当仅考虑第一项时,该模型仅确定正常深度并称为运动波路由。随着每个连续的近似水平,方程变得更容易解决,但失去了一些表示真实现象的能力。
在某些情况下(NOAA,2000),建模者已经开发出一些方法,可以在特定条件下关闭方程式中的繁琐术语,同时在大多数时间将它们留在解决方案中。
扩散类比
在扩散类比或扩散波(Ponce,1986)中,连续性和动量方程组合成单个方程
其中c=运动波速度(ft/s,m/s);
D=波的衰减系数(ft2/s,m2/s);
系数c和D最好从观察到的水文图估计,并且可以按常规渠道计算
其中T =顶部宽度(m,ft)
当斜率相对较大且深度较小时,扩散类比效果很好。系数c通常被称为运动波速度。
运动波
如果非稳态流动事件期间的条件没有明显偏离正常流动,则可以消除公式3.6右侧的大多数项以给出
该等式被称为运动波解。
当流量变化缓慢且阶段放电关系没有显着循环时,运动波路由工作良好。
马斯京根道路
一种常用的水文路线形式是马斯金根法,它假定在一个范围内的存储由下式给出
其中S =存储(ft3,m3)
K =存储常数(s)
X =确定存储时流入和流出的相对重要性
I =流入量(ft3 / s,m3 / s)
对于大多数流,X约为0.2,而K是到达范围内的行程时间的近似。在Linsley,Kohler和Paulhus(1982)中给出了基于场数据确定X和K的图形方法。虽然一般来说,运动波方法背后的理论使其更适合没有顶部而不是下水道的开放式通道,Samani和Jebelifard(2003)已经证明了如何通过一些修改将其应用于圆形管道。
距离的放电由下式给出
其中下标是指时间步骤1和2.时间步长的持续时间。系数由下式给出
作为检查,请注意
来自Muskingum Routing的典型流形图如图3.4所示。
图 3.4 流程路由实例
Muskingum-Cunge路由
Muskingum-Cunge方法是Cunge(1969)提出的Muskingum方法的一种变体,它使路由系数根据顶部宽度和流量的变化而变化。它结合了运动波方法的理想特征和马斯金根法的优点,因为它允许有限的衰减量。这种路由方法在Ponce,Li和Simons(1978),HEC(1990)和Yen中讨论过。 (2001年)。在管道流动问题中特别需要顶部宽度流量在一定范围内随流量的变化而剧烈变化.Muskingum-Cunge方法的流体力学方程的简化形式由下式给出
其中c =波动速度(ft / s,m / s)
u =水力扩散系数(m2 / s,ft2 / s)
qL=横向流入量(m3 / s,ft3 / s)
马斯金根系数可由下式给出:
其中Ax =距离stp(ft,m)(大约cAf)
T =顶部宽度(ft,m)
这可以求解(对于K = At和a = 1 2K,给出流量的以下关系
系数a由下式给出
凸路线
水文路线的另一个变化是凸路线,其仅使用来自前一时间步的流来确定从到达的流出(US Soil Conserva tion Service,1972)。流动方程是
其中c =凸路由系数
凸面布线系数与波速c不同(公式3.8)。它是时间步长与到达范围内的旅行时间的比率。时间步长应小于旅行时间(即c lt;1)。然而,行程时间不是常数,而是速度的函数。通常确定对应于最大流量的50%至75%的速度。系数由下式给出
其中V =代表速度(ft / s,m / s)
△t=时间步长(s)
L =管道长度(到达)(ft,m)
加权平移路线
虽然行程时间通常应大于时间步长,但有时会有一些非常短的管道会迫使时间步骤变得不切实际地变小。对于这种情况,当需要有一个在cgt; 1时工作的方法时,可以计算放电量
在具有陡坡的小型系统中,干扰基本上沿管道滑动而几乎没有衰减。为了确定给定时间的流量, 仅需要在位置VAt处提前一步查看流量的上游。该值很可能不在流已知的点之间的位置。因此,需要插值来确定通过下游的流量。
级别池路由
水平池路由(有时称为修改脉冲)不是管道路由方法,而是一种将流量路由到存储池或水库的方法。在下水道流动中,这可以应用于存储潮湿天气流的盆地。当头损不像存储量那么重要时,这种方法适用于模型元素。
方法摘要
表3.1总结了用于近似完整动态ecluatioris的方法,该表基于Haestad Methods等人(2003)中的类似表格。该表格列出了简化中所包含的假设以及何时适用。
一般来说,只要收集系统没有备份和流量反转,大多数对Saint-Venant方程的简化都可用于废水收集系统。在这种情况下,需要完整的Saint-Verdant exjuatioris。在设计情况下然而,工程师并没有建造下水道以便它们备用和反向流动,因此简化的布线方法工作正常。在小型系统中,即使是简单的布线方法也是不可能的,因为稳定的峰值流量分析通常是足够的。
路由方法的复杂性
虽然上一节中讨论的方法可以解释通道和管道不流动的不稳定流动,但真正的废水收集系统可能包括这些方法中未考虑的并发症。
lt;


