
英语原文共 19 页
本节所介绍的方法用于确保重力排水管道能够以一定的形状和密度来运送分散的颗粒。这些分析没有考虑沉积物的冲刷。为了使沉积物发生侵蚀,作用在固体材料上的水动力升力和曳力必须克服恢复力、浮重、颗粒之间的链接力和粘聚力。Delleur(2001)与Butler、May以及Ackers(1996)对下水道中泥沙的运输情况进行了更详细的分析。
考虑到近年来人们对于污水在下水道中的运动做了大量的研究。在2003年,Hudraulic Engineer出版了一期关于城市排水系统泥沙运动水力学的专刊。在这本书内,读者可以参考Asheley,Crabtree,Fraser和Hvitved-Jacobsen(2003);Butler,May,和Ackers(2003);Coleman,Fadele和Garcia(2003);Desutter,Rushford,Tait,Huygens,verhovern,andsaul(2003);Knigth and Sterling(2000);Ota 和Nalluri(2003);Pisano,Olsquo;Riordan,Ayotte,Barsanti,and Carr(2003);Rushforth,Tait和Saul(2003);Saul,Skipowrth,Tait 和Rushforth(2003):Tait,Chebbo,Skipworth,Ahyerre,和 Saul(2003)
2.10 比能和临界流
在明渠流动中,像比能、缓流、急流;流态(水面线?)、水跃和回水曲线一类的研究(话题)很重要。在生活污水管道特别是小管径中,流态的的几种情况在设计上有很重要的意义。
比能
在明渠流动中,比能的大小和槽底有关。
其中:
y——水深(单位,m)
V——平均流速(单位,m/s)
g——重力加速度(9.81m/s2)
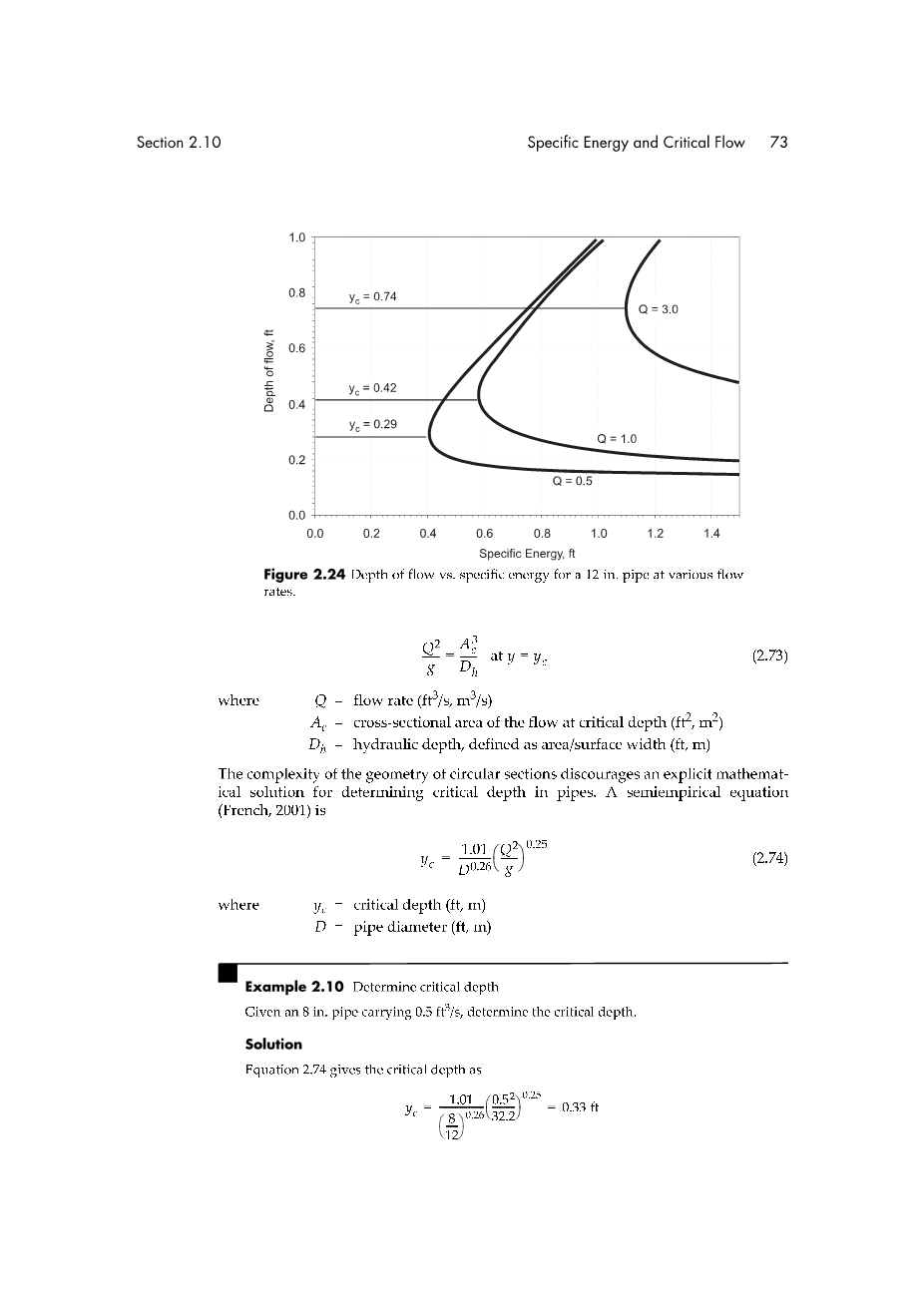
水流深度和比能量的关系图见2.24
一般来说,对于两种不同的水流深度可以存在相同的比能,这种情况被称为共轭深度。
对于给定的流量,出现最小比能的深度被称为临界深度(yc)。特别要注意的是当接近临界深度时,能量随深度变化而引起的变化幅度小,然而当比能不是最小值时,使深度发生显著变化则需要较大的能量。
上式2.72(比能)能够对y求导,以数值0来定义曲线上最低能量点,即临界深度。对于任何形如下图开口曲线的关系,可以用下式表示:
其中:
Q——流量(m3/s)
Ac ——临界深度时对应的的截面积(m2)
Dh——水力深度,用(面积/表面宽度)表示(m)
圆截面形状的复杂性使得用数学方法确定管道的临界深度有困难。一个(用于计算)的半经验公式(Freanch,2001)是
其中:
yc——临界深度(m)
D——管径(m)
例如2.10 确定临界深度
已知管径为8英寸,管道中流量为0.5ft3/s,求临界深度
解:
利用式2.74可以得到临界深度为
另外一种方法是通过y关于E的函数利用图线来确定yc。比能可表示为
其中
在0到0.667之间选择一个y的值,下图显示在y=0.33ft处有E有最小值。
弗劳德数
弗劳德数是流体中惯性和重力的比值,表示为
(2.75)
将式2.73中的临界深度带入式2.75中,我们可以知道在临界深度yc处弗劳德数为1。
亚临界和超临界流动
在正常的流动中,当水流深度大于yc时,弗劳德数小于1,称为亚临界流(或缓流),河道坡度较平缓。当水流深度小于yc时,弗劳德数大于1,这时被称为超临界流(或急流),坡度较陡。
亚临界流和超临界流的存在依靠管道的坡度决定。在多数管道中流态都是缓流或者急流。然而在一个范围狭窄的坡度中,流态通过流速和水深的增加量确定。
缓流可能存在于低流速(的情况),急流可能存在管道半满流(的情况下),同时当管道接近满流时又变为缓流。因此,对于特定的管道可以将坡度陡的用于一些流速而坡度缓的用于其他情况。
水跃
当水从下游急流变为下游缓流时,会发生一种水深的突然变化,即水跃。除非上游速度很快,水跃变化很小,一般而言,水跃只有几英尺高。在下水道中,当一个坡度陡的管道和一个坡度缓的管道汇合的时候会发生水跃。上游管道和下游管道是否发生水跃取决于流速和管道坡度。对于特定的管道(形状),水跃发生的位置会随着流速的变化而变化,因此在一个正常的流速范围内,水跃既可以发生在管道的上游也可以发生在管道的下游。
动量平衡脉冲原则可以描述水跃,这种关系可以表达为:
(2.76)
其中:
Q——容积流量(m/s)
rho;——密度(kg/m3)
V——矢量速度(m/s)
sum;F——作用在流体元上的矢量和,包括其重力(N)
通常,对于给定的流量,存在两个深度能够满足公式2.76,这些深度出现在水跃前后,被称为跃迁水深或共轭水深。
水跃在湍流中损失的能量,除了非常小的均匀流顺势外都能通过比能方程(公式2.72)来确定:
(2.77)
或
(2.78)
在封闭情况下中,有时下游的共轭水深“必需”比管道高度大。所以在水跃后,下游管道会充满轻微的压力。当这种情况出现在下水管道中时,除非在上游有极高的流速或巨大的流量,不然压力会很小并且通常不会超过几英尺水头。这种情况同样也代表流量超过了明渠管道中的水流容积。在这种情况下,水跃发生在上游检查井或者上游管道并且导致检查井积水。在下水道中,这种情况最可能出现在坡度平缓的地方。
另一个需要考虑的是水跃会引起湍流,湍流会释放如硫化氢一类的溶解性气体并且导致异味。为了更深入的讨论下水道中的水跃可以参阅Hager(1999)。
水面线
在明渠中流经一系列管道后,当水流逐渐均匀时,水面往往会发生深度的变化。多数深度变化出现在检查井水量变化的地方附近。水面通过这些变化深度确定的剖面称为水面线或者流量剖面;最常见的外形称为渐变流。水面坡度用dy/dx来表示,能量损失和水头损失的关系十分明显。粗化得到深度y作为沿管道距离x的函数。因为这些表达式的直接积分比较困难,一般采用有限步数值积分法求解。求有限阶跃方程的一种常用方法是:
管道1、2点的能量方程通过公式2.24表示:
这里再次写出
(2.79)
其中:
z——管底高度(m)
y——水深(m)
V——平均流速(m/s)
hL——单位能量损失(m)
注意公式2.79的关系
其中:
E——比能(m)
S0——管道坡度(m/m)
S——平均能量(m/m)
△X——管道长度(m)
公式2.79到2.83能够重新组合变形为:
(2.84)
公式2.84是描述渐变流中x,y关系的常用方法。其中的一个公式,比如曼宁公式,用来确定S,即估计平均能量线斜率的截面。一个整理过的曼宁公式经常被使用,其中Vm和Rhm是末端流速和水力半径的平均值,其形式为:
(2.85)
其中:
N——曼宁公式粗糙系数
Vm——1、2段流速的平均值(m/s)
Rhm——1、2段水力半径的平均值(m)
k——美式单位制取1.49,国际单位制取1.0
当考虑到表面轮廓曲线时,需要注意当水深大于yc水流为缓流。计算从下游水深控制点开始回到上游。相反,当水深小于yc时,计算从上游控制点开始向下游延伸。Haestad的方法和Durrans(2003)以明渠参考做出举例。
回水曲线
当流动条件由于管道几何形状的变化而偏离正常深度时,流动最终会接近一个新的正常深度。描述这种过渡到正常深度的水流形态被称为回水曲线。如果水流过渡是逐渐变化的,则可以用公式2.84确定过渡深度。如果流动过渡迅速,则该截面将经历急变流,这时公式2.84就不管用了,因为水头损失和深度之间没有关系不明确。水跃就是水流急剧变化的例子。水流通过临界深度时会发生快速变化。
大多数下水道系统设计模型会计算回水曲线,尽管在大多数情况下,流量在管道形状改变后很快接近正常情况。当下游的水深比下水道中正常的流动深度更深时,回水曲线更有可能会在大直径下水道的下游末端出现:例如,排到湿井的管道。在这种情况下,可以在上游方向计算回水曲线,以确定回水影响的范围。
图2.25是排入一口湿井的下水管道的剖面图。需要注意的是,在102.3英尺高处的湿井中的下游水会导致管道内的水流回流,从而导致回水效应延伸到上游管道。地面标高的计算从下游标高(102.3英尺)开始,一直持续到上游管道末端。这种情况下,正常深度为1.82英尺,上游水深为1.86英尺,所以回水效益在整个管道内延伸。
2.11 水流控制的水工设施
在卫生和组合下水道中,可以使用各种结构来限制水流或将水流分成两部分。水流可以从下水道分流,以进行适当的贮存和处理,也可以溢流到受纳水体中。常用的控制结构包括孔、堰、虹吸和闸门。美国土木工程师学会(1992)和水环境联合会(1999)编写的实践手册讨论了这些结构的设计。本节回顾用于计算流经这些结构的水流的基本方程。
一些系统可能又类似的溢流下水道,这些下水道是由于上游负荷超过下水道的容量而安装的。对于这些分流,不存在“水流控制结构”。这些相识的下水道,或者在某些情况下,(可以)由一个等效的下水管道代替,这些类似的下水道相同的水头损失与流量关系。
明渠中的流量控制结构,尤其是用于测量流量的结构,由Bos(1976)和French(1985)发现。不幸的是,实际下水道中的结构往往不完全符合理想的实验室堰和孔(的情况)。水环境联合会(1999)对其中一些结构进行了阐述,Hager(1999)对这些结构的流动方程进行了讨论。
孔口
孔可以用来测量或控制流量。在下水道中,它们方向是水平或垂直的,如图2.26所示。由于它们通常排出流量小,孔经常与其他控制结构结合使用。通过一个孔的流量取决于该孔的面积,孔上的有效水头,以及该孔的边缘(形状)。这些变量之间的关系可以表达为:
(2.86)
其中:
Q——排放流量(m3/s)
Cd——排放系数(取决于孔的边缘)
A0——开孔面积(m2)
g——重力加速度(9.81m/s2)
hc——有效水头(m)
Brown, Stein和Warner(2001)指出,如果孔口开口的边缘是均匀的且是正方形,则Cd=0.60。对于粗糙的边缘,比如使用乙炔焊炬切割的口所产生的边缘,应使用Cd=0.40。
孔口上的有效水头取决于它是自由的还是浸没在水中的(垂直的孔还是水平的孔)。如果水流为自由落体(靠重力流动),则有效水头为上游水面标高与孔口中心标高之差。如果下端水淹没了孔的出口,有效水头与孔口上游和下游的水面高度差相等。
堰
在下水道内可以找到各种形状的堰,如图2.27、2.28和2.29。堰通常分为尖顶堰和宽顶堰。一个相对较薄的板块形成了尖顶堰的顶部。对于宽顶堰来说,堰顶厚度相对较大,且过堰顶的水流为缓流。
其他类型的堰的属性与堰顶形状(矩形、三角形、梯形)和堰的末端是否有水流收缩(有关)。收缩的堰导致水流的收缩。受抑制或不受约束堰上的水流没有末端收缩。
尖顶矩形堰
尖顶堰上的流量可以通过能量方程确定。该过程相当于将堰上游的总能量头与堰顶的总能量头相等。以上游能量等级表达的排放方程取决于堰的横截面形状,同时不可避免地还包括一些简化的假设。为了简化假设和修正理论流量,引入了经验流量系数Cd。
在一个完全收缩的矩形尖顶堰(没有底部和边缘影响)中,可以用堰头上的高度H表示:
(2.87)
其中:
Cd——流量系数
L——堰顶长度(m)
H——堰顶水头(m)
式中假设的堰上游水流的速度水头可以忽略不计,因此堰上的水头H为上游水面与堰顶的高程差。
从根本上说,式2.87中的流量系数取决于流动的雷诺数和韦伯数(i.e,粘性和表面张力可以忽略不计)在无量纲水头处,其中为渠道底部以上和堰顶之间的高度,如图2.30所示。然而实验表明流量系数可以用下式表示(Rouse, 19462 Blevins, 1984)。
(2.88)
当比值小于5时,表达式的结果是准确的。当=10时,表达式结果近似。当>15时,能够通过假设临界流方程(Chaudhry,1993)来计算。
当流动发生在一个收缩的矩形堰上时,末端的收缩


