
英语原文共 23 页,剩余内容已隐藏,支付完成后下载完整资料
14
双向板:弹性和屈服线分析
14-1钢板弹性分析综述
在这里简要回顾了板坯弹性分析中涉及的概念,以显示板中的载荷和内部弯矩之间的关系。 此外,甚至更重要的是,这将显示弯矩和板面曲率之间的关系。
厚板可分为厚板(厚度大于跨度的十分之一),薄板(厚度小于跨度的四分之一)和中厚板。 厚板将一部分载荷作为平拱传递并且具有明显的面内压缩力,结果内部抵抗压缩力C大于内部拉力T.薄板通过作用传递一部分载荷作为张力膜; 因此,T大于C.中等厚度的板不具有拱作用或膜作用,因此具有T = C。
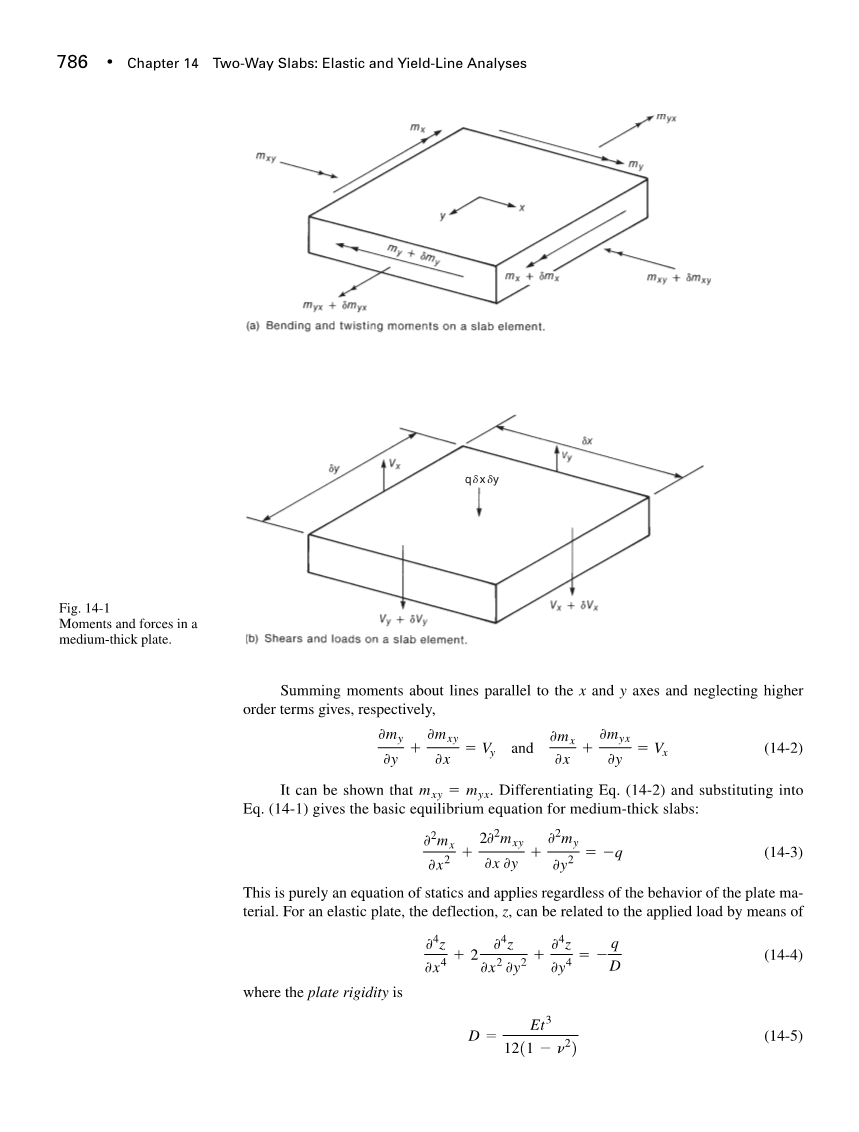
图14-1显示了从中等厚度的双向板切下的元素。 该元件受图14-1a中所示的弯矩以及图14-1b中所示的剪切和载荷的作用。 (为清楚起见,图中的数字是分开的。)
在每个边上存在两种类型的弯矩:弯曲力矩mx和my围绕与边缘平行的轴线,以及围绕垂直于边缘的轴线的扭矩mxy和mYX。 时刻由双头箭头表示的矩矢量表示。 有问题的弯矩根据右手螺丝规则对箭头起作用。 矢量的长度表示弯矩的大小。 矢量可以通过图形或数字添加。 矩形mx等等是为它们所作用的边缘的单位宽度定义的,剪切Vx等等也是如此。 mx和my矩是正的,对应于顶面上的压缩。 如图14-1a所示,相邻边缘上的扭矩都会导致在两个边缘之间的拐角处板的同一表面上产生压缩。
总结垂直方向上的力
q d x dy
图14-1中厚板的弯矩和剪力
对平行于x和y轴的线和忽略高阶项求和的弯矩分别给出
可以证明mxy= mYX。 区分方程 (14-2)并代入方程 (14-1)给出了中厚板的基本平衡方程:
这纯粹是一个静力学方程式,适用于任何板材的行为。 对于弹性板而言,挠度z可以与施加的载荷相关联
钢板刚度在哪里
其中n是泊松比。 术语D与板的单位宽度的EI值相当。
在弹性板分析中,Eq。 (14-4)求解以确定偏转z,并且矩从中计算
其中z是正向下的。
14-2 从有限元分析设计弯矩
解决方程式的最常用方法 (14-6)将使用有限元分析。 这种分析给出了每个元素中的mx,my和mxy的值,其中mx,my和mxy是每单位宽度的矩。 图14-2显示了由对角线裂缝限定的一部分元素。 图14-2b显示了来自有限元分析的x和y面上的力矩。 关于与裂纹平行的轴的时刻是mc,由下式给出
这块板要在x方向和y方向用具有正力矩mRX和mRY每单位宽度的钢筋加固。 与假想裂纹平行的轴的相应力矩容量为
其中mRC必须等于或超过mc以提供足够的强度。 等同这些和解决最低限度,我们得到
其中k是一个正数,fnof;mxyfnof;意味着m的绝对值xy。 这对于所有的裂纹方向都是正确的(即,对于所有的k值)。 随着k增加,mRY下降,mRX上升。 两者之和中最小的一个(即最小的总钢筋)取决于所讨论的板,但k = 1是各种力矩值的最佳选择[14-1],[14-2]。
在每个方向的板坯底部的钢筋设计为提供正向力矩抗力
设计在每个方向的板的顶部加固,以提供负弯矩阻力
当使用mRX和mRY的值计算板坯中正弯矩钢筋(底部钢筋)的面积时,计算基于公式 (14-10a)或等式 (14-10b)。 这些方程中的 符号和绝对编号组合在一起形成术语“ |” mxy|“正值。 如果mRY或mRX在这两个方程中都是负数,那么在设计底部钢筋时将它们设置为零。
mRX和mRY - 负矩的计算。 对于负弯矩钢筋(顶钢),计算基于方程式。 (14-10c)和(14-10d)。 - 符号和绝对数字相结合,使术语“ - |” mxy|“负值。 如果在这两个方程中mRY或mRX都是正数,那么它们在设计顶部钢筋时设为零。
例14-1在某一点上计算设计弯矩
钢板底部的钢材:
钢板顶部:
gt;
由于mRX为正,因此在设计钢板顶部的钢板时将其设置为零。 ■
通常,钢筋在正交带内均匀分布,
在一个频带中提供的总增强足以抵抗为该频带计算的总系数矩,并且
如在有限元分析中计算的那样,频带中的每单位宽度的时刻电阻至少是频带中每单位宽度的最大弯矩的三分之二。
在直接设计方法中,钢筋的宽度取决于ACI代码13.2节中定义的钢筋和中间钢筋的宽度。 这种带(带)宽度的使用通常是可以接受的。
14-3板材屈服线分析:
在超载条件下,如果一块楼板弯曲失败,钢筋将首先在高转矩区域屈服。 当发生这种情况时,板的这部分起到塑性铰的作用,只能抵抗它的铰接弯矩。 当负载进一步增加时,铰接区域将发生塑性转动,并且由于附加负载而产生的力矩会重新分配到相邻的部分,从而导致它们屈服,如图13-4所示。 已经发生屈服的带称为屈服线,并将板分成一系列弹性板。 最终,存在足够的屈服线以形成塑性机构,其中板坯可以塑性变形而不增加施加的载荷。
板坯的屈服线分析方法实际上在荷载效应分析和构件强度分析之间带来了更多的连续性。 在一般设计中,使用适当的载荷系数和强度降低因子,将弹性分析中的力矩和剪切力与塑性构件强度进行比较。 在板坯屈服线方法中,开发塑性机构所需的载荷直接与构件的塑性阻力(名义强度)进行比较。 载荷因子和强度降低因子可以包含在程序中,正如后面的一些例子所示。
屈服线分析使用刚性塑性理论来计算与板的各个部分中给定的塑性弯矩阻力相对应的失效载荷。 它没有给出任何关于挠曲或屈服首先开始的荷载的信息。 尽管1921 - 1923年A. Ingerslev首先提出了产量线分析的概念,
KW Johansen开发了现代屈服线理论[14-3]。 这种分析广泛用于斯堪的纳维亚国家的板坯设计。 此处介绍的屈服线概念有助于理解服务负载和故障之间的板行为。 更多细节在[14-4]至[14-7]中给出。
屈服准则
为了限制挠度,楼板通常比挠曲要求厚得多,因此它们很少有配筋率超过方程(1)中定义的平衡配筋率的0.3到0.4倍。 (4-25)。在这个配筋率范围内,
图14-3收益标准。
力矩曲率响应本质上是弹塑性的,塑性力矩容量保守地假定为等于该截面的设计挠曲强度fMn。
如果屈服发生在与钢筋成一定角度alpha;的直线上,如图14-3所示,假定弯曲和扭转力矩沿着屈服线均匀分布,并且是弯曲和弯曲力矩的最大值屈服线交叉的加固层。 进一步假定钢筋在穿过屈服线时没有扭结。 在图14-3中,x和y方向的增强件提供了每单位宽度(k-ft / ft)的mx和my的弯矩容量。 弯曲力矩mb和扭转力矩mt,单位长度屈服线可以从单元的力矩平衡计算出来。 在这个计算中,a将从x轴逆时针测量; 如果在板底部产生张力,弯矩mx,my和mb将为正; 如图所示,如果矩矢量指向远离截面,则扭矩mt将为正。
考虑图14-3b中元素的平衡:
这些公式仅适用于正交加固。 如果mx= my,则不管屈服线的角度如何,这两个等式都减小到mb= mx= my和mt= 0。 这被称为各向同性增强。
t
轴和屈服线的位置
屈服线形成在最大矩的区域,并将板分成一系列弹性板段。 当屈服线形成时,所有进一步的变形都集中在屈服线上,并且板通过长铰链连接在一起的一系列刚性板发生偏转,如图14-4所示。 如图14-5所示,变形模式由沿线支撑和柱上的轴线以及屈服线控制。 由于各个板围绕轴线和/或屈服线旋转,所以这些轴线必须笔直。 为了满足图14-4中A和B点的变形的相容性,
A B
图14-4带屈服线的板变形。
正矩收益线
正矩收益线
负片屈服线
负片屈服线
图14-5屈服线模式的例子。
分割两块板的屈服线必须与那些板旋转的轴相交。 图14-5显示了受到均匀载荷的许多板坯的轴线和屈服线的位置。 图1和2中的产量机制。 14-4和14-5被称为运动学允许的机构,因为相邻板段的位移和旋转是相容的。 如果对于一个给定的板坯面板可以定义不止一种运动学允许的机制,则应调查每种机制以确定哪一个机制导致对给定负载的最小面板抗性。
图14-6在四条边上简单支撑的平板中的屈服线。 (照片提供G.麦格雷戈。)
图14-6显示了与图14-4所示板坯类似的钢筋混凝土板的下侧。 裂缝倾向于遵循正交增强模式。 从角部延伸的宽裂纹和沿板中部的宽裂纹带标记正屈服线的位置。
解决方法
在选择运动学允许的屈服机制之后,可以计算支持给定载荷组所需的m值,反之亦然。 解决方案可以通过均衡方法来实现,其中为每个板段编写平衡方程,或者通过虚拟工作方法,其中板坯的一些部分被给予虚拟位移并且考虑结果工作。
当使用平衡方法时,必须非常小心地显示作用在每个单元上的所有力,包括扭矩,特别是当几条屈服线相交或屈服线与自由边相交时。 在这样的位置,在屈服线的交点处需要偏置的垂直节点力。 由于节点力量可能会被赋予错误的符号或位置,因此一些建筑规范要求通过虚拟工作方法来完成屈服线计算。 介绍性介绍仅限于解决方案的虚拟工作方法。 关于平衡方法的更多信息可以在[14-3]至[14-7]中获得。
虚拟工作方法
一旦选择了屈服线,板上的某个点就会被赋予虚拟位移d,如图14-7c所示。 当这个数量变化时,负载所做的外部工作是
q =区域元素上均匀分布的负载
d =该元件的偏转
W =板块上的总载荷
cent;c=该段质心的偏转
在例14-2中,将显示方程(1)的右边。 (14-13)可以表示为板坯屈服机制的位移体积的q倍。
总的外部工作是每个板块完成的独立工作的总和。
旋转屈服线完成的内部工作是
u =与虚拟位移对应的屈服线处的角度变化,d在虚拟位移过程中完成的全部内部工作是在每条单独的屈服线上完成的内部工作的总和。 因为假定屈服线在施加虚拟位移之前形成,所以在虚拟位移期间不会发生弹性变形。
虚拟工作原理指出,为了节约能源,
外部工作=内部工作
虚拟工作解决方案是一个上限解决方案; 也就是说,负载W等于或高于真实的故障负载。 如果选择了一组不正确的屈服线组,W对于给定的m将太大,或者相反,对于给定的W,m的值将太小。
例14-2通过虚拟工作单向板的屈服线分析
将分析图14-7中显示的单向板,以确定将导致故障的面积负载qf。 图14-7a显示了钢筋加固,假设的失效机理如图14-7b所示。 当使用本章中所有板的平面图时,支撑处的交叉阴影表示法表明板或者固定在支撑处或者在支撑处连续,并且板能够抵抗负弯曲。 单阴影符号将用于指示不能抵抗负面时刻的支持(即简单支持)。 假设左支撑的负弯曲能力mn1等于6 k-ft / ft,右支撑的负弯曲能力mn2等于10 k-英尺/英尺 在中跨附近的板筋的正弯曲能力mp等于4k-ft / ft。
选择轴和屈服线。 如图14-7b所示,两个板块的负屈服线(如虚线所示)和旋转轴必须位于支撑处。 因为支撑处的两个轴线彼此平行,所以中间附近的波浪实线所示的正屈服线必须平行于支撑物,以便成为运动学允许的机制。 导致qf的最小值的距离x将被确定。
给板块一个虚拟的位移。 假设正屈服线C-D向下移动一个等于虚拟位移d的距离,如图14-7c所示。 这导致板段I旋转角度uI,并且板段II旋转角度uII。 跨越中跨附近正屈服线的总旋转是总和,uI uII。 对于小位移,u近似等于tan u,所以
内部工作是板坯段偏转时塑性铰区内矩的总和。 所有的力矩容量都是每英尺长度的,所以这些值需要乘以塑料铰链的长度,这等于板坯宽度b。
请注意,瞬时值现在以kips表示,而不是k-ft / ft。
计算外部工作。 正如在Eq。 (14-13),这可以计算为每个板块(板)的矢量力的总和乘以板的质心的相应位移的总和,或者作为面积力qf乘以被置换的体积为假定的机制。 这两个程序将在这里使用。
对于第一个过程,两个板块都是矩形的,所以它们的质心将处于中间长度。 另外,因为每个段在一端被支撑并且偏转一个距离d,在另一端,每个质心将偏离d / 2的距离。 作用于质心的等效矢量力等于面积负载qf乘以该区域的面积。 从而,对于第二个程序,板坯机构的位移体积等于图14-7c中位移形状的三角形面积乘以板坯的宽度。
因此,外部工作的表达是
如预期的那样,这两个程序给出了相同的结果。 对于某些板坯分析案例,一个过程可能比另一个更容易,因此建议设计师熟悉这两个过程。
等同于外部和内部的工作。 设置EW = IW并求解qf。 注意
虚拟偏转d始终会在等号上消除。 在这种情况下,平板宽度也会从表达式中消除。
在这种形式下,qf的解决方案将以ksf为单位。
求解qf.的最小值qf的最小值可以通过
但对于更复杂的双向板问题则是一个迭代解决方案
程序可能会更有效率。 电子表格可用于交易。 由于
全文共12369字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[12771],资料为PDF文档或Word文档,PDF文档可免费转换为Word


