
英语原文共 11 页,剩余内容已隐藏,支付完成后下载完整资料
数字调制解调器内插 - 第11部分:实施和性能
Lars Erup, Member, IEEE, Floyd M . Gardner, Fellow, IEEE, and Robert A. Harris, Member, IEEE
摘要—早前的一篇论文介绍了数字接收机中的数字插值理论背景,并且描述了内插器控制方法。本文基于多项式理论,介绍了特定等级的内插滤波器的特性。本文简要地较少了内插滤波器的应领域,其应用之一是为实际的硬件设备的设施提供了便利。
经过模拟仿真可以看出,具有简单结构的内插器却具有出色的性能。在多数情况下,采用两点间线性插值是足够的。如果需要更好的性能,可以使用经典的四点间的三阶多项的插值滤波器。具有分段抛物线脉冲的新式四点插值滤波器比标准立方体插入器操作更简单,性能更加的优越。
第一部分介绍的基于NCO的控制方法与传统锁频环路等效,其操作过程通过模拟仿真验证。
Ⅰ.引言
本文的第一部分[1]提出了数字信号数字插值的基本方程:
(1)
其中{x(m)}是以间隔Ts取得的信号样本序列,并且h I(t)是时间连续的模拟内插滤波器的有限持续时间脉冲响应的虚部。(1)中的数字操作式在可调间隔Ti
内释放内插值y(k) ,通常情况下,Ti与Ts相等。
公式(1)中的参数为:滤波器的索引i = I1到I2,基点索引m k(其标识I = I2-I1 1用于第k个插值的信号样本),以及分数区间mu;k(其识别I滤波器系数(1)中用于第k个插值)。
第一部分在宽泛的范围内假定了内插滤波器的理想特性; 但它仍然需要评估和选择特定的滤波器响应以应用于实际的调制解调器。 本文在第II节中探讨了简单多项式滤波器 —一类包括经典插值的多项式—的性质。
本文第III节研究了用于执行(1)中计算的若干数字结构,并进行了讨论。
本文第四部分对上述的滤波器进行了模拟仿真,用来评估它们对调制解调器性能的影响,并得出了结果。结果表明,极其简单的内插器可以用于调制解调器性能,并且其影响可忽略不计。
第五节阐述了基于[1]中设计的NCO方法的完整定时控制环路的设计,介绍了如何直接采用用于设计锁相环路的相似技术。
II.基于多项式的过滤器
插值滤波器可以基于多种函数。一类函数是基于多项式的滤波器的函数,其中连续底层滤波器[1]的脉冲响应hI(t)是t(或其替代物pk)中的多项式或分段多项式。 此多项式脉冲响应与下面讨论的相关的近似或内插多项式完全不同并且应将二者区分开来。
基于多项式的滤波器本质上不是最优的选择; 接下来阐述其受到重视的几个原因:
- 多项式插值是多项式滤波器的一个比较小但比较重要的子类,现存有大量相关文献。
- 基于多项式的滤波器容易进行描述。
- 基于多项式的滤波器具有良好的滤波器特性。
- 下文描述的特殊的FIR结构可以对简单滤波器系数的处理。 但该结构仅适用于多项式滤波器。
连续时间内的近似多项式k(t)与每个基于多项式的滤波器相关联,它近似于t = kTi附近的x(t)。(1)中的插值滤波器计算此多项式的样本y(kTi)= pk(kTi)。对于每个I点基点集{x(m)}来说,近似多项式都是不同的。pk(t)是否为x(t)的较好的近似值不重要;调制解调器的内插器可以对信号执行过滤。大多数情况下,不需要对近似多项式进行明确的分析(2)。
- .插值多项式
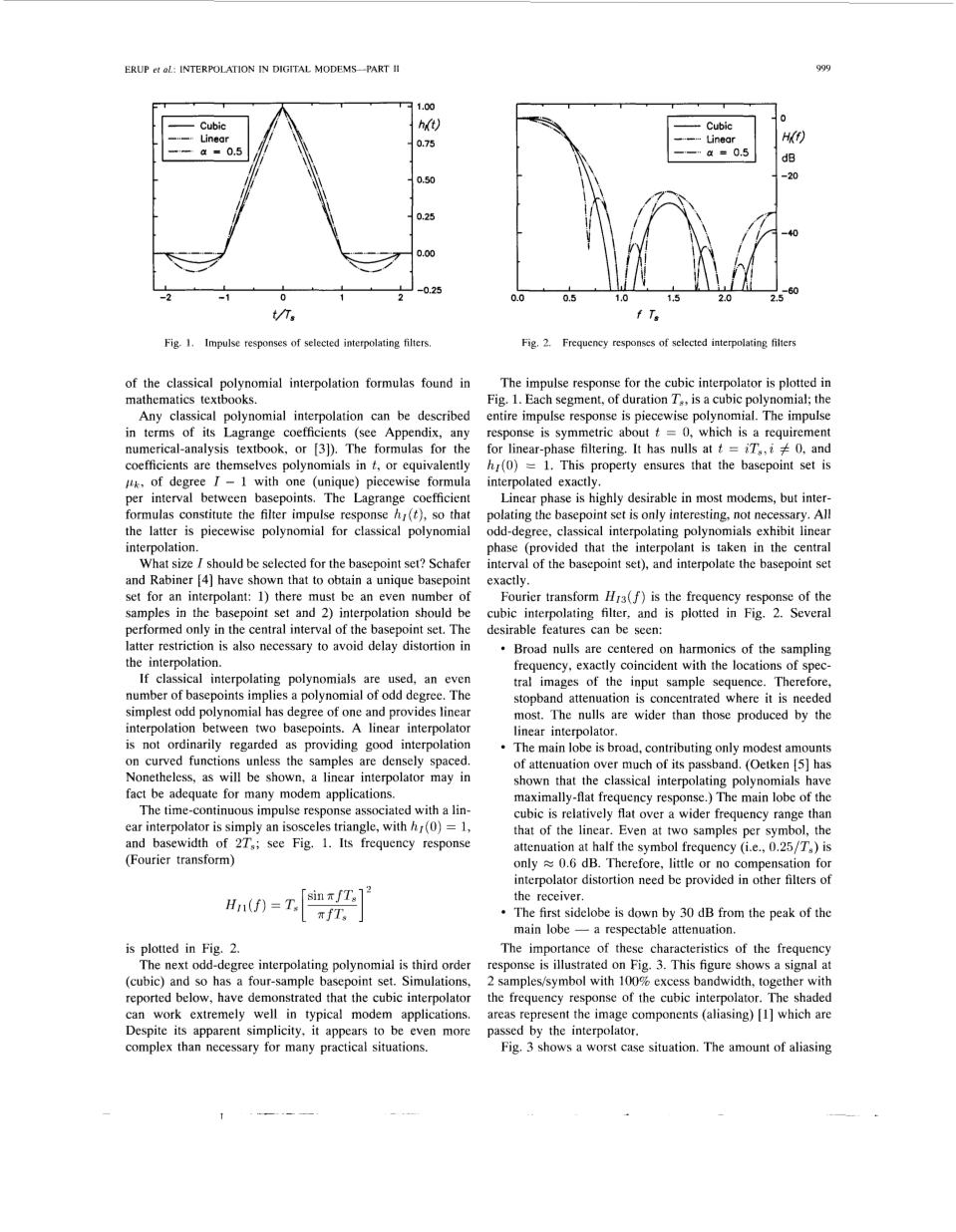
图1 图2
作为一个特例,如果第k个基点集的所有I点和所有k的pk(mTs)= x(mTs),则称pk(t)为内插多项式。 这种情况包括所有数学教科书中的经典多项式插值公式。
就拉格朗日系数而言,任何经典的多项式插值都可以进行描述(见附录,任何数值分析教科书,或[3])。系数本身就是t中的多项式,或等价于mu;k,或相当于程度I-1的每个基点间隔中的(独特的)分段公式。拉格朗日系数公式构成滤波器脉冲响应hI(t),所以后者是经典多项式插值的分段公式。
对于基点集来说I应为多大的尺寸?Schafer和Rabiner [4]表明若想在一个插值中获得独立的基点集:1)该基点集合的样本必须为偶数 2)插值只能在基点集的中心区间执行。第二点对于避免延迟失真插值是必要的。
如果使用传统的插值多项式,则偶数基点数则为奇次多项式。最简单的奇次多项式的度数为1,并提供两个基点之间的线性插值。通常认为,除非样本间隔密集,否则线性内插器在曲线函数中不能呈现良好插值。尽管如此,事实上,线性内插器适用于许多调制解调器的应用。
与线性插值器相关的时间连续脉冲响应只是一个等腰三角形,其特征为hI(0)=1,基本宽度为2Ts;见图1.其频率响应(傅里叶变换)展示在图2中。
下一个奇次内插多项式是三阶(立方),因此有四个样本基点集。下文进行的模拟证明了立方体插入器在典型的调制解调器应用中可以很好地运行。尽管它显得简单,但在实际情况下会比所需的更复杂。
图一展示了三次插值器的脉冲响。持续时间为Ts的每段都是三次多项式;整个脉冲响则为分段多项式。冲动响应是关于t=0对称的,这是线性相位滤波的一个要求。它在t = iTs,ine;0,hI(0)=1的情况下为空值。此属性确保基点集是完全内插的。
线性相位在大多数调制解调器中是非常理想的,但是插入基点集合只是有趣的,而不是必需的。 所有奇次经典插值多项式都呈现出线性相位(前提是插值取自基点集合的中心间隔),并准确插入基点集合。
傅里叶变换HI3(f)(图二)是三次插值滤波器的频率响应。图二中可以看到几种理想特性:
·宽零点集中在采样频率中的谐波上,与输入样本序列的光谱图像的位置完全一致。 因此,阻带衰减集中在其最理想的地方。 这些零点比由线性插值器生成的零点更宽。
·主瓣宽广,比起其通带而言,只产生了适当的衰减(Oetken [5]表明经典插值多项式具有最平的频率响应)。在更宽的频率范围内,立方的主瓣比线性的主瓣相对平坦。 即使每个符号有两个采样点,在符号频率(即0.25 /Ts)一半处的衰减是只有asymp;0.6 dB。因此,接收器的其他滤波器基本不需要补偿内插器的失真。
·第一个旁瓣由主瓣的顶峰下降了30 dB——这是一个可观的衰减。
这些频率响应特性的重要性如图3所示。该图显示了一个信号带有100%过剩带宽的2个样本符号,以及三次内插器的频率响应。阴影区域代表图像组件(混叠)[1],它们是由插入器传递。
图3
图3显示了最坏的情况。通过减少过多的信号带宽,增加采样速率或设计内插器使其在0.5 / Ts和1 / Ts之间具有更尖锐的滚降,可以减少混叠的现象。
- 替代多项式
描述hI(t)的多项式不是必须的度I-1。例如,可以减少计算负担在四点插值器中使用二次方程式hI(t)的分段,而不是立方体表达式由拉格朗日公式提供.
考虑到欲望给予的限制内插基点集,线性相位(偶对称)并要求直流增益(系数之和)为独立于mu;k,单个设计参数alpha;仍然存在表征分段的二次方程式。改变一个线索到不同的内插器响应。系数的细节公式在附录中提供。
图1显示了对应于alpha;= 0的脉冲响应(线性内插器)和alpha;= 0.5。“ 频率分段抛物线插值器的响应广泛地类似于立方体(图2)。对于某些特定的值然而,在一个频率上出现额外的零和旁瓣低于F,= 1 / Ts,. 通过改变alpha;,可以进行折衷在主瓣的滚降陡峭和陡峭之间这个第一副瓣的水平。 此行为可以调整为使来自第一信号图像的混叠量最小化。
- 其他选择
凭借简单的多项式,为什么在不同的过滤器中会成为首选?
1)可设计出色的滤波器功能; 见[6]例子。他们可能是更高程度的插值多项式或非插值多项式,或者完全是非多项式函数。
2)在一些结构中,下面将要描述的是上级过滤功能不需要更多的在线计算相同长度的劣势功能。
III.过滤结构
可以确定两种类型的实施:
- 预先计算并存储滤波器脉冲的采样值响应hI(t)。加载I存储的样本—过滤器系数—从存储器转换为横向滤波器每个插值。
- 直接在线计算插值而不存储脉冲响应采样,或者甚至可能没有明确计算脉冲响应。(似乎仅适用于基于多项式的滤波器。)
这些替代品的特点如下。其他观点可以在[6]中找到。
- 存储的冲动响应
系数存储器将通过期望的分数间隔mu;k来解决。将脉冲响应存储在有限的区域中记忆要求mu;k被量化,称为L均匀间隔。结果,恢复的时钟受到时间的影响抖动Ts/ L,相对于信号波形的峰峰值。
将会有I·L字的bI位存储在每个字中记忆。对于每个插值,必须有bI位的I个字转移到过滤器结构。传输总线可以很容易随着我或bI的增长超过微不足道而变得过于宽泛尺寸。传输总线的宽度可能构成强大的障碍至少实际实施一个存储的脉冲响应适用于传输必须完全满足的高速应用平行。
实现仅依赖于结构参数L,I,和bI,而不是hI(t)本身,它仅由组成存储在内存中的号码。计算负担是独立的hI(t); 优越的滤波器特性不需要更多的努力而不是具有相同结构参数的较差的一个。任何过滤器功能可以被采用; 存储响应方法不限于多项式.
存储的过滤器样本完全等同于水龙头一个多相滤波器的系数[7],每个L抽头和I个抽头系数相同。每个抽头对应一个不同的量化值峰mu;k。一个多相实现可以替代这个存储过滤器实现,过滤器增加了L倍硬件。多相滤波器相当于一组滤波器,如[8]中所述。
- 在线计算
如果所有的计算都是在线执行的,那就是不需要滤波器系数存储器也不需要量化这是强加的。所有计算都可以执行在使用的机器的本地字大小中,只有这样由此字大小施加的量化。
下面介绍直接插值的三个示例。所有都限制为基于多项式的滤波器。因为已经发现了使用非多项式过滤器进行直接高速插值的方法是不可行的。
一种直接的方法可能是评估滤波器系数(例如,来自拉格朗日公式)作为每个的mu;k的函数个别插值。 特别简单的公式,或低在大多数情况下需要速度或高并行性来快速完成这种方法。线性插值或四点分段抛物线脉冲响应提供简单的公式,非常适合快速直接评估滤波器系数.
第四部分和第五部分描述的模拟采用直接评估滤波器系数,因为操作速度原因不是最重要的。
虽然滤波器特性是任何插补器的基础,不限制计算滤波器系数可以设计出令人满意的方法。这不是必要的脉冲响应在内插器中明确可见结构体。目标是产生插值,而不是构建过滤器。例如,可以通过执行线性插值简单的公式
(2)
作为另一个例子,牛顿的方法是一种教科书方法[9],它直接计算插值信号样本的画面及其差异。在牛顿的方法,从不计算滤波器系数(也不是多项式pk(t)的系数)。然而,相同的插值可以像基点样本一样获得已应用于适当的过滤器。 牛顿的方法是方便从表格数据手动计算。
另一种方法,更适合用于信号插值机器,由Farrow [l0]设计。让冲动响应为每个T中的分段多项式的Ts字段,z = I1至I2:
(3)
用(3)代入(1)并重新安排术语来表明插值可以从中计算。
(4)
系数bl(i)是固定的数字,与mu;k无关,仅由滤波器的脉冲响应hI(t)确定。所有脉冲响应分段由相同次数N的多项式描述.
等式(4)本身就是一个多项式mu;k。嵌套评估(4)是最有效的方法。对于三次插值:
(5)
图4
(4)的硬件评估框图如图所示图4.这个Farrow结
全文共10403字,剩余内容已隐藏,支付完成后下载完整资料
资料编号:[16968],资料为PDF文档或Word文档,PDF文档可免费转换为Word


