基于卫星的中国珠江三角洲地区PM2.5区域加权回归模型外文翻译资料

 2021-11-27 09:11

英语原文共 7 页

基于卫星的中国珠江三角洲地区PM2.5区域加权回归模型

Weize Song,Haifeng Jia,Jingfeng Huang, Yiyue Zhang

清华大学环境学院，北京100084

美国马里兰大学地球系统科学跨学科中心

文章信息

文章历史:

2014年5月16日收到文章

2014年8月7日收到修改后的表格

2014年8月7日通过审核

2014年9月1日网上发表

关键词：PM2.5；卫遥感；气溶胶光学深度；地理加权回归；珠江三角洲地区

摘要

为在区域尺度上估算卫星立交桥地面PM2.5日浓度，建立了基于卫星的地理加权回归(GWR)模型。该模型考虑了PM2.5的空间变化和非平稳性，提高了PM2.5的估计精度。利用2012年5月至2013年9月珠江三角洲地区PM2.5数据对该模型进行了评价和验证。评价结果表明，在吸收气象参数的情况下，GWR模型能够解释地表PM2.5浓度变异性的73.8%，优于传统的两种统计模型(一种是一般线性回归模型- i, 56.4%;一种是半经验模型- ii, 52.6%)。星载AOD垂直校正与相对湿度显著改善了AOD - pm2.5的相关关系。研究结果表明，GWRmodel在区域PM2.5估算中具有巨大的潜力和价值。

1. 介绍

许多流行病学研究表明,细颗粒物质与空气动力学直径小于2.5mu;m (PM2.5)是伴随着不利人类健康的影响,如呼吸道疾病和心血管疾病(见Balasubramanian amp;, 2008;Donkelaar等，2010;Lim等人，2011)。因此，地面PM2.5浓度的测量对于解决公众健康问题非常重要。虽然静态环境监测点的测量通常被认为是准确的，但其数据频率和质量一致性往往限制了连续空间监测(胡et al.， 2013)。另一方面，基于复杂过程的空气污染模型往往受到自然资源和人为排放清单信息不完整的阻碍(Koelemeijer, Homan， amp; Matthijsen, 2006;Dawson等，2007;Pelletier等，2007;田和陈，2010)。

近年来，遥感技术被广泛应用于空间PM2.5监测(Wang and Christopher, 2003;刘等，2005;Donkelaar等，2006;Jia amp; Liu, 2006)。利用卫星获取的气溶胶光学深度(AOD)，可以实现大区域PM2.5的估算。卫星获得的AOD测量了卫星立交桥期间气溶胶颗粒对柱状光的消光(Tian amp; Chen, 2010)。在许多能够获取AOD的卫星传感器中，分辨率成像光谱仪(MODIS)提供了质量最可靠的长期气溶胶数据记录之一(Chu et al.， 2002;Engel-Cox, Holloman, Coutant， amp; Hoff, 2004;Kaufman, Tanre， amp; Boucher, 2002;Lee, Liu, Coull, Schwartz， amp; koutakis, 2011;Levy, Remer, Mattoo, Vermote， amp; Kaufman, 2007;Remer等，2005;Yap amp; Hashim, 2013)。

为了探索卫星获取的AOD与地面实测PM2.5之间的定量关系，开发了各种模型，如半经验模型(Koelemeijer et al.， 2006)、混合效应模型(Lee et al.， 2011);Yap amp; Hashim, 2013)，广义加性模型(Paciorek, Liu, Moreno-Macias， amp; Kondragunta, 2008)，交替条件期望(ACE)模型(Benas, Beloconi， amp; Chrysoulakis, 2013)，人工神经网络(ANN)模型(Gupta amp; Christopher, 2009;和一般线性或非线性回归模型(Donkelaar et al.， 2010;Liu, Franklin, Kahn， amp; koutakis, 2007)。此外，建议将气象地理因素纳入AOD-PM2.5关系中，提高模型性能(Guo et al.， 2009;刘，Paciorek， amp; koutakis, 2009;田和陈，2010)。然而，上述模型的估计精度仍有提高的空间(De Leeuw et al.， 2006)。没有充分考虑AOD-PM2.5关系的空间变异性，即AOD-PM2.5相关性的强度不应该在空间上是恒定的，而应该随着空间环境的变化而变化(胡et al.， 2013)。基于局部回归技术的GWR模型可以检验空间变异性和非平稳性(Fotheringham et al.， 1996;赵，杨，周，2010;胡等，2013)。

本文首先利用气象参数(相对湿度、温度、风速)建立了两种基于卫星AOD的常规模型，在区域尺度上估算PM2.5浓度。其次，引入并发展了新的GWR模型，推导出AOD-PM2.5关系。为了定量评价模型的性能，以珠江三角洲地区为例，将模型PM2.5与地面实测数据进行对比。最后，对上述三种模型的估计精度进行了比较。并利用GWR模型对卫星反演的PM2.5进行了空间分布分析。

2. 数据和方法

2.1.数据

2.1.1.卫星检索大气气溶胶数据

MODIS搭载在NASA Terra和Aqua卫星上，MODIS气溶胶产品提供了10公里空间分辨率下大气气溶胶颗粒的柱状光学特性观测。质量保证最好的MODIS AOD产品(quality flag = 3)被认为在华东地区范围内满足最低的不确定性容限(Levy et al.， 2010;熊等，2005)。此外，与珠江三角洲地区地面CE318太阳光度计测量结果(Li, Mao， amp; Liu, 2005)相比，MODIS气溶胶数据(收集5.1级产品)的平均精度大于80%。研究还发现，利用垂直修正方程可以对原始AOD进行修正，使其与地面实测PM2.5的相关性更好(Koelemeijer et al.， 2006;田和陈，2010):

纠正AOD=AOD/BLH (1)

在5.1 MODIS暗目标2级气溶胶反演中，地面产品在550 nm处的大气气溶胶是从NASA LAADS网站(http://ladsweb.nascom.nasa.gov/)获得的。本研究采用质量保证最好的optical_depth_land__ocean数据层(大气气溶胶质量标志= 3)。为珠江三角洲地区(纬度范围[21°17])。6′-23°55。，经度范围[111°59]。7′-115°25。3rsquo;))，2012年5月至2013年9月，分别从Terra和Aqua采集到357张MODIS大气气溶胶图像和319张MODIS AOD图像。为了增强PM2.5区域变异性的对比，利用克里格法将10 km MODIS 大气气溶胶数据重采样到5 km空间分辨率网格。

2.1.2.地面测量PM2.5数据

2012年5月至2013年9月珠三角地区地面实测PM2.5数据来源于中国广东环境信息发布平台(http://www.gdep.gov.cn/)。研究区内共有37个监测站，采用锥形单元振荡微天平(TEOM)法获得每小时地面PM2.5浓度值(Wang, Chen, Tao, Zhang， amp; Su, 2010)。因此，颗粒加热至50℃后的“干”PM2.5测量值可能低估了蒸发导致的气溶胶颗粒质量(Tian amp; Chen, 2010)。修正后的PM2.5()可由以下相对湿度(RH)修正方程得到(Koelemeijer et al.， 2006;田和陈，2010):

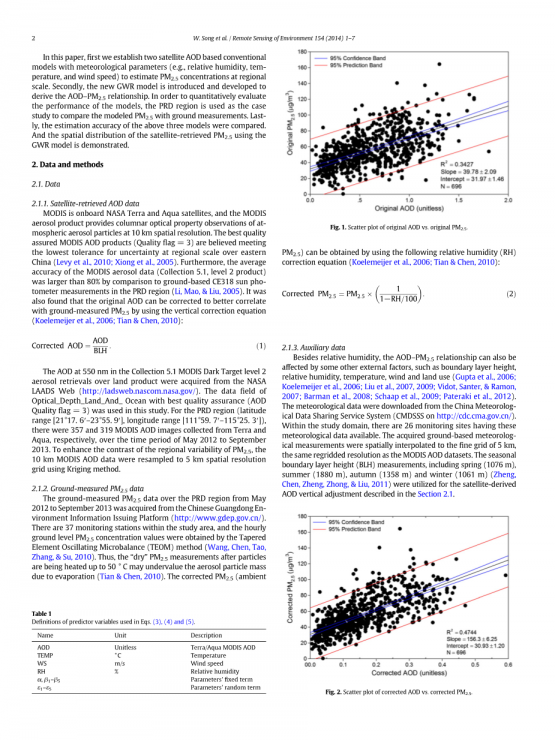
图1所示。原始AOD与原始PM2.5的散点图。

2.1.3。辅助数据

除相对湿度外，边界层高度、相对湿度、温度、风和土地利用等外部因素也会影响AOD-PM2.5关系(Gupta et al.， 2006;Koelemeijer等，2006;刘等，2007,2009;Vidot, Santer， amp; Ramon, 2007;Barman等，2008;Schaap等，2009;Pateraki等，2012)。气象数据从中国气象数据共享服务系统(CMDSSS on http://cdc.cma.gov.cn/)下载。在研究范围内，共有26个监测站提供这些气象数据。所获得的地面气象测量数据在空间上插值到5公里的精细网格中，其重增分辨率与遥感AOD数据集相同。利用春季(1076 m)、夏季(1880 m)、秋季(1358 m)、冬季(1061 m)等季节边界层高度(BLH)测量值(Zheng, Chen, Zheng, Zhong， amp; Liu, 2011)对卫星获得的AOD垂直平差进行了2.1节描述。

图2所示。校正AOD与校正PM2.5的散点图。

2.2。方法

2.2.1。传统的统计模型

作为颗粒组成和垂直剖面变化的指标，敏感影响因子(如相对湿度和温度)可以显著影响卫星反演AOD与地面实测PM2.5的相关性(Liu et al.， 2007)。为了在区域尺度上有效地描述这些预测因子与PM2.5之间的数值或定量关系，我们建立了两个传统的统计模型:一般线性回归模型(称为模型- i)和半经验模型(模型- ii)。并与前人建立的相似模型和后一节提出的GRWmodel进行了比较。

模型- I可表示为式(3):

包括AOD、TEMP、RH和ws。这种关系定义为一般的线性回归形式，与前面在介绍中提到的一些论文中相同。此外,合适的系数(如alpha;,beta;1,beta;2beta;3,beta;4)和随机错误(例如sigma;1、sigma;2,sigma;3sigma;4,sigma;5)表1中列出并解释了。

模型- II为半经验模型，可表示为式(4)，由数据驱动，相关理论对其进行塑造(Liu et al.， 2007;田和陈，2010)。因此，假设PM2.5与AOD、风速(WS)、温度(TEMP)、相对湿度(RH)呈非线性关系。而AOD与ws具有幂律函数关系

图3所示。模型一的实测与拟合PM2.5的散点图。

AOD、TEMP、RH与PM2.5呈指数关系(Liu et al.， 2007)。

其中PM2.5为左侧因变量，为地面监测仪日监测浓度。右侧的预测变量包括AOD、TEMP、RH和WS。参数(alpha;和beta;1minus;4)表示回归系数和随机sigma;1错误,sigma;2,sigma;3,sigma;4和sigma;5分别。

为了便于参数化(Tian amp; Chen, 2010)，降低数据分布的偏态性(Liu et al.， 2007)，将式(4)对数化为线性回归形式，如式(5)所示。

以上预测变量汇总如表1所示。

2.2.2.地理加权回归(GWR)模型

已有研究表明，AOD-PM2.5相关性在空间上存在显著差异，并随空间环境的变化而变化。这种关系的空间变异性导致使用全局常数参数的模型精度较差(Engel-Cox et al.， 2004;胡等，2013)。GWR是一种在区域尺度上检测参数值连续曲面空间变化和非平稳性的实用技术(Brunsdon, Fotheringham， amp; Charlton, 1996;佛瑟林厄姆，查尔顿，amp;布伦斯顿，1996)。本研究利用GWR模型，每天为每个PM2.5监测点生成局部R2。利用自适应带宽对监测点的不均匀分布进行计算，然后对模型的残差进行空间自相关分析。

GWR模型可表示为式(6):

将GWRmodel中的预测变量在5 km的精细网格上进行空间插值，得到与Terra/Aqua MODIS AOD数据相同的空间分辨率。具体GWR是利用ArcGIS软件中“spa -势统计工具”的“地理加权回归”函数计算的。然后，为了可视化研究区域PM2.5年浓度的空间分布，利用ENVI软件中的“band math”工具，基于每日卫星获取的PM2.5地表数据集进行叠加计算。

图4所示。模型- ii中观测到的PM2.5与拟合PM2.5的散点图。

3.结果与讨论

3.1。探索性分析

图1为原始AOD与PM2.5之间的一般线性回归关系，与图2中校正后的AOD与PM2.5的线性回归结果相似。这两幅图都表明，如果采用简单的线性回归方法，卫星反演的AOD对R2为0.34或0.47的PM2.5具有潜在的估计价值。R2值从0.34显著提高到0.47，说明AOD的垂直修正(详见2.1.1节)和PM2.5的相对湿度修正(详见2.1.2节)可以显著提高模型性能。与图1相比，图2的相关斜率更高(156.3plusmn;6.25 vs. 39.78plusmn;2.09)，数据点更集中于回归直线附近。两个回归拦截关闭(分别为31.97plusmn;1.46,30.92plusmn;1.2),表明31mu;g / m3是总体均值最低背景地面卫星大气气溶胶观测PM2.5浓度阈值在研究领域在研究期间。但是，以AOD为唯一预测变量的两种回归模型的确定系数(R2)都相对较低。这意味着AOD-PM2.5关系也会受到其他因素的影响，如气象条件和空间环境(Kumar, Chu， amp; Foster, 2007)。

3.2.模型结果与验证

3.2.1模型- I和模型- II

式(3)中描述的模型- I是使用模型训练数据集(N = 680)开发的，并使用验证数据集(N = 358)进行评估。综合来看，同化气象预报因子的模型具有显著的相关性(p b 0.01)，能够解释相应日PM2.5浓度变化的56.4%(表2)

R2增长9%。换句话说，从目前的分析来看，其他的预测因子(例如温度和相对湿度)

原文和译文剩余内容已隐藏，您需要先支付 30元 才能查看原文和译文全部内容！立即支付

以上是毕业论文外文翻译，课题毕业论文、任务书、文献综述、开题报告、程序设计、图纸设计等资料可联系客服协助查找。

您可能感兴趣的文章