
英语原文共 8 页,剩余内容已隐藏,支付完成后下载完整资料
在定子磁链同步坐标系下永磁同步电动机直接转矩控制系统的最大转矩电流比控制
Tatsuki Inoue, Yukinori Inoue, Member, IEEE, Shigeo Morimoto, Member, IEEE,and Masayuki Sanada, Member, IEEE
摘要
本文提出了在定子磁链同步坐标系下,永磁同步电动机直接转矩控制系统的最大转矩电流比控制,定子磁链矢量可在M-T坐标轴系表示,考虑到PMSM磁饱和交互耦合效应,需要在很多复杂的数学模型上使用转子同步(d-q)坐标系。在M-T坐标系中,
MTPA控制的数学模型只需要三个参数,这三个参数只需要由三个测量的点确定。这个方式的有效性可以通过实验数据来证明。
关键词:交流电机驱动,直接转矩控制(DTC),最大转矩电流比(MTPA),永磁电机,同步电机驱动
1.介绍
永磁同步电机(PMSM)驱动在工业设备和家用电器中广泛的应用,在PMSM驱动中,电流控制通常都在转子同步坐标系中。在d-q坐标系中,PMSM的最大转矩电流比(MTPA)控制规律可作为一种有效控制[1]。然而当需要高功率及转矩密度时,有必要实现转矩的增加或减小大小,然后出现在PMSM中的磁饱和和耦合效应会是显著的,并且电机参数变化取决去电枢电流[2]。参数的变化影响着控制转子位置和速度传感器驱动的能力。总而言之,当涉及到高功率和高转矩密度时,高效控制在d-q坐标系中不容易实现。因此,需要一种新的方法来解决磁饱和问题。磁饱和和耦合效应已经在很多研究中检验了[2]-[6]。d轴和q轴电感分别受d轴电流分量和q轴电流分量的影响,并且已经在内置式永磁同步电机(IPMSM)、面装式永磁同步电机(SPMSM)和同步磁阻电机(SynRM)中进行建模和评估[6]。永磁同步电动机的精确模型往往有很多参数,并且确定这些参数需要花费很多功夫。
直接转矩控制(DTC)是一种结构简单的控制技术[7]。它可以应用于任何种类的电机,因此有很多关于基于DTC控制的PMSM驱动系统[8]。一般来说,DTC运用于d-q坐标系的数学模型中来实现大范围速度内高效运行。因此,这种DTC运行方式需要磁通和磁感应强度的测量数值,这也导致控制性能与电流矢量控制没有什么区别,因为两者都是使用相同的数学模型。此外,这个在d-q坐标系下的数学模型可能不适合基于DTC控制的电机驱动系统,因为DTC运行基于静止alpha;-beta;参考坐标系。因此,一个数学模型只单独适合DTC是最理想的,DTC可以在定子磁链同步(M-T)坐标系中执行,因为磁通矢量可以估计。M-T坐标系可以被运用于PMSMs、IPMSMs、SynRMs和感应电动机(IMs)[9],[10]。在[11]中,报道了一种高效控制方法,这种方法适合基于DTC的SynRM驱动系统,并且[12]报道了在M-T坐标系中弱磁和转矩限制的控制方式。在M-T坐标系中,弱磁控制方法只需要电枢电阻作为电机参数并且对电阻和电感的变化不敏感。
本文提出了一种基于DTC的PMSM驱动系统的MTPA控制系统,第二部分写出了MTPA曲线新的数学模型的推导来解决磁饱和效应。一种决定MTPA曲线三个参数的方法已经在[13]提出。按照习惯,用一个查找表来进行MTPA控制,但是这需要很多数据点的测量和存储。这里提出的新型控制方法,基于所推导出的DTC系统中的MTPA曲线数学模型,这个方法只使用三个参数,这些参数仅由三个测量的MTPA运行点决定。
图1 alpha;-beta;、d-q、M-T坐标下的矢量图
图2 -平面下电枢电流轨迹
第三部分描述了MTPA控制中参考磁通的计算方法。在第四部分中,实验结果证明了该方法的有效性即解决了磁饱和。
2.MTPA曲线的数学模型
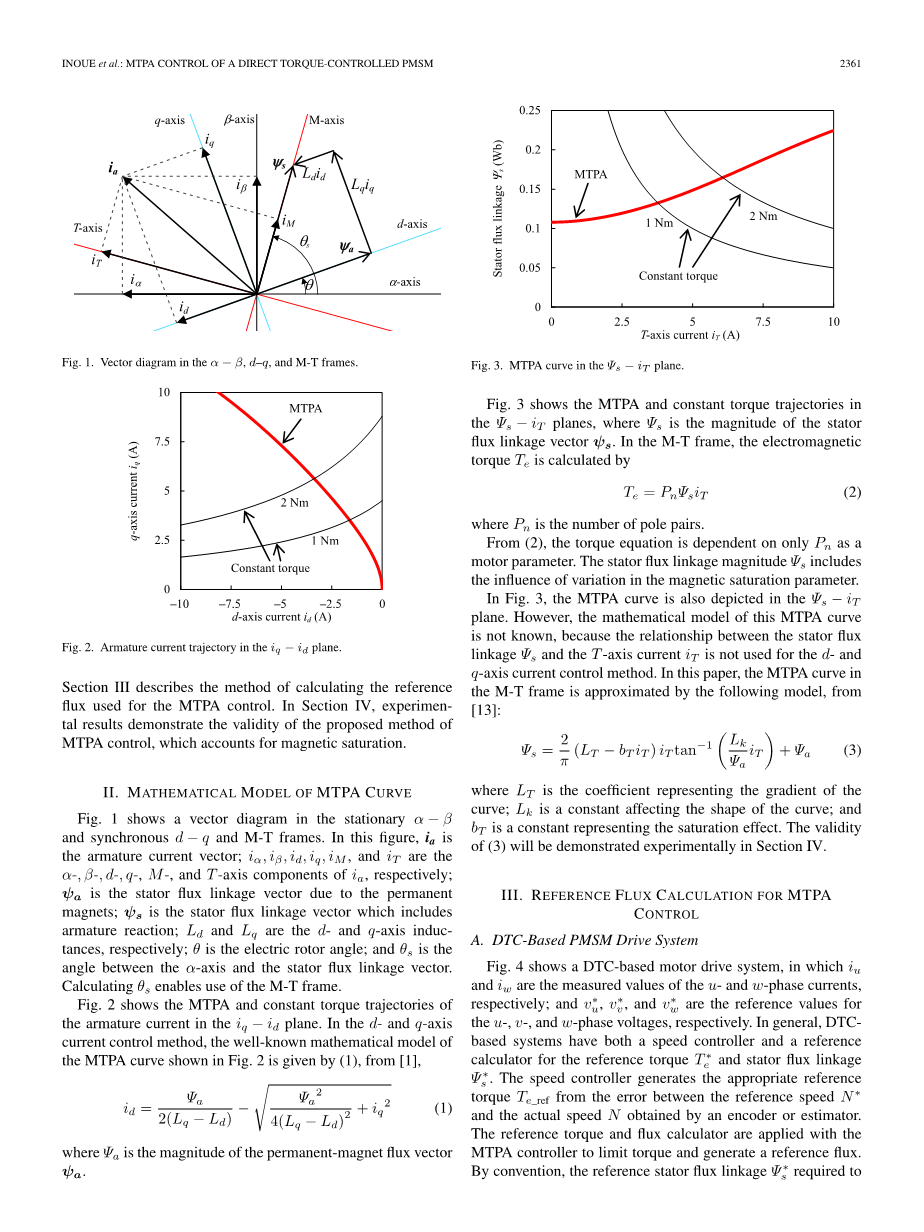
图一显示了在静止alpha;-beta;坐标系、同步d-q坐标系和M-T坐标系下的矢量图,在此图中,是电枢电流矢量,、、、、、分别是在alpha;轴、beta;轴、d轴、q轴、M轴、T轴上的分量,是由永磁体产生的定子磁链矢量,是包括电枢反应的定子磁链矢量,和分别是d轴和q轴的感应系数,theta;是转子电角度,是alpha;轴和定子磁链矢量的夹角,计算可以使用M-T坐标系。图2显示了MTPA和电枢电流在-平面的恒转矩轨迹,在d、q轴电流控制方式中,在图2中最著名的MTPA曲线数学模型得自[1],从[1]有
(1)
是永磁体磁链矢量的大小
图3 MTPA曲线
图三显示了在-平面上MTPA和恒转矩轨迹,是定子磁链矢量的大小。在M-T坐标系中,电磁转矩:
(2)
是极对数
在(2)中,转矩方程里只有是电机参数,定子磁链大小包括磁饱和参数变化的影响。在图3中MTPA曲线也在-平面中绘出,但是,MTPA曲线的数学模型是未知的,因为定子磁链和T轴电流的关系不适用于d轴和q轴电流控制方式中。在本文中,在M-T坐标系中的MTPA曲线是由一下模型近似,来自[13]:
(3)
是曲线的梯度系数,是个影响曲线形状的常数,表示磁饱和效应的常数,(3)的正确性将在第4部分得到实验演示。
3.MTPA控制参考磁通量的计算
图4 DTC电机驱动系统图
A.PMSM的DTC系统
图4显示了基于DTC的电机驱动系统,其中和分别是是u相和w相电流的测量值,,和分别是u.v.w相电压的参考值。一般来说,DTC系统为参考转矩和参考定子磁链设有一个速度控制器和一个参考计算器。速度控制器通过参考转速实际转速N和的差值产生近似参考转矩,转速由译码器或估测器得到。参考转矩和磁通量计算器应用于MTPA控制器中来限制转矩并产生参考磁通。按照惯例,用来决定MTPA的参考定子磁链是通过参考转矩查找表得出,因为和不能获得一个实时计算。相比之下,所提到系统,可以由(3)算出,但是,(3)没有转矩但有T轴电流,因此,在这个部分中,我们提出了一种方式来估测M-T坐标轴系,并且提出了一种方法从参考转矩
来得到即通过T轴电流。
B.M-T坐标系的估算
DTC系统可以利用M-T坐标系,因为定子磁链矢量可以估算,alpha;轴和beta;轴定子磁链和:
(4)
和 (5)
和分别是是alpha;轴和beta;轴的电枢电压,和分别是是alpha;轴和beta;轴的电枢电流,是电枢电阻。
根据(4)、(5),得T轴电流,定子磁链,转矩:
(6)
(7)
(8)
图5显示了有T轴电流观测器DTC框图。
C.所提出模型的MTPA控制方法
图6显示了所提出方法的MTPA控制,从(2)中,在-平面中恒定参考转矩曲线是通过下式绘出:
(9)
图5 含T轴电流观测器DTC框图
图6 所提出的MTPA控制
如图6所示,MTPA条件下的定子磁链在一点与定子磁链相同,这点是由(9)得到的恒参考转矩曲线与由(3)得出的MTPA曲线的交点。
但是,(3)中的反正切使之很难计算出和运用下面的技术。从(9)中-平面的反比例曲线看出,随增加而减小。在一方面,(3)中,随增加而增加。因此,在图6,在MTPA条件下的T轴电流必须在和之间。在本文中,所提出的方式使用和的平均值作为一个合理点来接近MTPA条件。
图7 MTPA控制框图
图7显示了MTPA控制框图,尽管初始值与实际值不同,会在几个控制时间收敛于。
4.试验结果
- 试验系统
在表1中显示的PMSM参数,我用来评估(3)并提出MTPA控制,图8 展示了试验系统,PMSM驱动系统基于一个参考磁链矢量计算器(RFVC)DTC。(4)(5)中的积分代替一阶滞后滤波器,alpha;轴和beta;轴参考电压用于(4)和(5)磁通估算,逆变器的直流母线电压是150V。由于逆变器停滞时间,电压误差的补偿方法被应用。在实验系统中,用在速度控制器的实际速度N通过增量编码器测量。在控制面板中,RFVC DTC是100mu;s,调速器,参考转矩,定子磁链计算器的控制时间是5ms。
B.确定参数
(3)式需要的三个参数、和可由实验PMSM三个运行点确定,[13]中提出决定这些参数的方式总结在这部分中。
首先,永磁体产生的定子磁链通过测量空载下的感应电压来获得。第二,当gt;0时,表面负载转矩已运用,和此时由MTPA运行点计算出。MTPA点的测量通过寻找满足任何负载转矩下使电枢电流最小的。图9显示了几个满足MTPA条件的测量点。实验PMSM转子转速是1000,实验PMSM的运行点总满足MTPA条件,因为电枢电压低于逆变器的最大输出电压。
表1 实验PMSM参数
任意两个MTPA运行点和,和计算
(10)
和分别是点和在T轴上的值,和分别是点和对应的定子磁链。
对于MTPA计算,理想情况是在点的T轴电流接近额定T轴电流的一半,点的T轴电流大于等于额定T轴电流。在图9中,运行点、分别对应额定转矩的40%和120%。
最后,是通过额外测量一个MTPA点确定,因为和是的函数,如(10)所示。图10表示了和对的关系。由于和能由确定,MTPA近似曲线可以通过代入额定值、和到(3)中得到。
为了确定的最小测量值,我们选择一个零界MTPA点,然后,的值跟随零界MTPA点选择。图11显示了近似MTPA曲线的例子,到的变化基于的变化。在MTPA曲线点表示150%额定转矩的情况下,是5mH或0.01mH。
图8 实验PMSM系统框图
图9 满足MTPA条件的测量点
图10 MTPA曲线斜率和磁饱和效应与影响MTPA曲线形状的常量的关系
图11 不同下的MTPA曲线
然而,还有一种理想情况,、和可以通在近似MTPA曲线和测量点间使误差最小化来确定,在MTPA曲线和测量点间的定子磁链误差平方根如下:
(11)
n是测量点的数量,和分别是T轴电流和第j个测量点的定子磁链,是定子磁链,将带入(3)得:
(12)
从(10)-(12),由每个计算出。图12表示了对应每个的误差,从图12中可以看出,定为5mH,因为误差在=5mH是有最小值1.34mWb,因此,可以将正确的代入(10)得到和,如图10所示,参数设定为=5mH,=89.3mH,=3.31mH。
图13表示了将确定的参数代入(3)后的MTPA曲线与测量点的比较,这个图形证明了(3)式正确的绘出MTPA曲线。
图12 影响MTPA曲线的常量
图13 (3)式所得MTPA曲线与测量点的比较
C.所提出方式和传统的查表法比较
查表MTPA控制和提出的MTPA控制特点已经由实验证明,图14显示了当负载转矩为线性时的控制特点,图14(a)表示了转矩响应,证明了测试电机电磁转矩跟随参考转矩,图14(b)显示了定子磁链的结果,图14(c)显示了在-平面中的控制轨迹,从图14(c)中,很明显的可以看出所提方式可以控制MTPA曲线的轨迹。
图14 所提方式的实验评估:(a)转矩响应,(b)定子磁链响应(c)-平面控制轨迹
通过该方式的计算得到的参考磁通近似于满足MTPA条件的定子磁链,因此,当参考转矩突然改变,很难维持精准的暂态MTPA曲线,因为和误差变大。图15显示了参考转矩突然变化的情况,测试电机在500速度下运行,参考转矩的突然转变是由于参考速度从500变到2000。图15(a)显示了测量的转矩会跟随参考转矩,即使突然变化,但是,图15(b)显示在3ms,该方式产生了一个参考定子磁链,这个参考磁链与查表所得不同,这是因为在参
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[141837],资料为PDF文档或Word文档,PDF文档可免费转换为Word


