
英语原文共 8 页
非线性粘滞阻尼单自由度体系的动力学
作者: Gloria Terenzi 1
摘要:本文分析了非线性粘滞阻尼对单自由度(SDOF)结构系统动力响应的影响。这种阻尼表征了一类特殊的流体粘滞阻尼器,最近在振动控制领域中用作基础隔离装置或包括在框架结构的钢支撑中的粘弹性元件。用于再现流体粘滞阻尼器的机械性能的分析关系是速度的分数幂律,其指数范围在0.1和0.2之间。这个函数之前已根据佛罗伦萨大学进行的特殊实验调查结果进行了校正。经典的线性粘滞单自由度振荡器的动力学在此基于上述分数粘滞阻尼(FrVD)关系重新表述。特别地,在自由和强制振动条件下检查瞬态和稳态响应。对于不同的阻尼水平,分析地确定放大率和传递率因子。此外,还定义了粘滞阻尼系数与频率比(即动态负载与振荡器频率之比)之间的关系。描述这些函数的图表提供了阻尼以及系统的弹性特性和动态作用的频率之间的直接相关性。
前言
近年来已经提出了旨在降低动态作用对结构的影响的各种装置。根据管理与瞬态环境事件相关的能量的方法,主要结构保护系统可分为三类。第一类是隔震装置(Skinner等人,1993),例如弹性体或铅-橡胶支座,以及滑动-摩擦摆体系。被动消能装置(Gluck等人,1996; Soong和Dargush,1997),如金属阻尼器,摩擦阻尼器,粘弹性阻尼器,调谐质量阻尼器和调谐液体阻尼器,属于第二类。最后,第三类包括半主动和主动控制系统(Soong和Constantinou 1994)。流体粘滞阻尼器起着特殊的作用,虽然通常被视为被动消能元件(Pekcan等人1995; Soong和Dargush 1997),但也可用于基础隔震(Makris 1992)。本文将关注这类阻尼器,特别是所谓的“Jarret弹性体弹簧阻尼器”(Soong和Dargush 1997; Datry等人1998),由一个钢筒和在内的一个交替作用于特殊的硅基弹性体材料的无孔活塞组成(Grenier 1991; Terenzi 1994; Pekcan等1995; Soong和Dargush 1997)。这些元件的主要特征在于它们可以设计成在纯阻尼器和弹性元件的两个极限条件下获得所需的任何粘弹性行为。此外,可以制造分别仅以一种或两种运动方式起作用的单作用(SA)或双作用(DA)装置。在粘弹性行为的一般情况下,弹性响应被激活超过特征阈值,该特征阈值由最初施加到材料上的预应力载荷确定。当动态作用终止时,该特性对活塞起到重新定位效果。
最近通过佛罗伦萨大学(Terenzi 1994; Chiarugi等人1995)和布法罗大学(Pekcan等人,1995)进行的实验调查研究了单作用和双作用流体粘滞装置的机械响应。 为了模拟观察到的阻尼行为,制定了分数粘滞阻尼(FrVD)关系,并根据试验结果进行了校准。
在本文中,对具有FrVD特性的单自由度(SDOF)元件的动力学进行了全面的论述,以建立分析含有流体粘滞阻尼器的体系的理论基础,作为基础隔震或被动控制(阻尼支撑)装置。 参考动态负载的频率内容检查分数粘滞阻尼单自由度体系的瞬态和稳态响应特性,然后将用分数模型开发的数值试验得到的结果与在具有相同刚度和等效阻尼的线性粘滞阻尼(LVD)模型上进行的平行研究的结果进行比较,讨论两种模型的响应之间的相关性和差异。关于稳态响应,从数值查询计算各种阻尼水平的放大率和传递率函数,其中假定正弦动作为输入以获得等于[0,5]的beta;(beta;=piv;/omega;1; piv;=正弦荷载的循环频率; omega;1= 2pi;/T = 具有基本周期T的单自由度体系的循环频率)范围。在这些分析中,选择损耗因子eta;作为参考阻尼参数; 实际上,如第三部分所示,在非线性阻尼问题的情况下,阻尼比xi;(定义xi;=cv/ccr=cv/2radic;(km),对应质量为m,刚度为k,阻尼系数为cv和临界阻尼系数为ccr的LVD振荡器)是没有意义的。 基于这些发现,本文提出了放大和传递函数的解析表达式,同时建立表征FrVD模型的阻尼系数c与beta;和eta;参数之间的关系。在结构应用领域中,这个关系要能直接估算考虑的这个FrVD-SDOF体系的c值,以便达到期望的阻尼效果。
流体粘性装置的机械性能
对两种类型装置试验的回顾
为了定义包括流体粘滞阻尼器在内的结构系统的动力学,人们关注SA粘弹性装置,它代表了Jarret弹性体弹簧阻尼器的基本类型。 事实上,DA元件衍生于SA装置,即采用一种移动其一端使其能够对张力做出反应的特殊外壳(Pekcan等,1995)。 作为这种制造过程的结果,DA装置的粘弹性响应严格地取决于衍生出它的SA元件的行为。
为了形成能够模拟SA元件动态特性的分析模型,下文将介绍佛罗伦萨大学(Terenzi 1994; Chiarugi等,1995)在纯阻尼器( PD)和粘弹性阻尼器(ED)上进行的试验的综合结果。通过比较检查这两种类型的装置的内部结构(图1),主要的视觉差异表现为只有PD活塞杆伸出活塞头并穿过整个外壳。尽管如此,在两种情况下,内圆柱形壳体都填充有硅基弹性体材料并加压到预定水平。当加载阻尼器时,通过压缩弹性体将活塞头驱入气缸。因此,一些材料可自由地围绕活塞头处的环形空间流动。阻尼特性严格依赖于孔口效果,当活塞速度减小到零时,弹性体围绕活塞头的流动停止,从而使得材料的压力在活塞的两侧均衡。
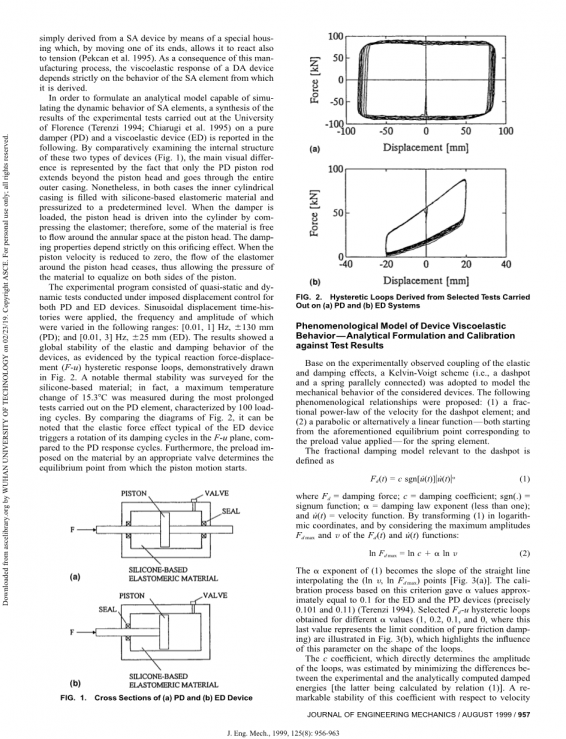
实验程序包括在PD和ED设备的强制位移控制下进行的准静态和动态测试。应用正弦位移时间历程,其频率和幅度在以下范围内变化:[0.01,1] Hz,plusmn;130mm(PD);和[0.01,3] Hz,plusmn;25 mm(ED)。结果表明,设备的弹性和阻尼性能具有全局稳定性,典型的反作用力-位移(Fu)滞后响应循环就证明了这一点,如图2所示。对有机硅基材料已进行了显着热稳定性测量。实际上,在对PD元件进行的最长时间测试期间测量的最大温度变化为15.37℃,其特征在于100次加载循环。通过比较图2的图,可以注意到,与PD响应循环相比,ED装置典型的弹力效应触发其在F-u平面中的阻尼循环的旋转。此外,通过适当的阀门施加在材料上的预载荷决定了活塞运动开始的平衡点。
图1.PD和ED装置的截面图
图2.在(a)纯阻尼和(b)粘弹性阻尼体系的选定测试得出的滞回环对比
装置粘弹性性能的唯象模型 - 对试验结果的分析公式和校准
基于试验观察到的弹性和阻尼效应的耦合,采用Kelvin-Voigt方案(即缓冲器和弹簧并联)来模拟所考虑的装置的机械性能,提出以下现象学关系:(1)速度的分数幂律——缓冲器元件;(2)抛物线或线性函数——两者均从对应于所施加的预载荷值的上述平衡点开始——弹簧元件。
与缓冲器相关的分数阻尼模型定义为:
(1)
其中Fd —阻尼力;c —阻尼系数;sgn(.)—正负号函数;alpha;—阻尼速度指数(小于1);—速度函数。通过在对数坐标中变换式(1),并考虑Fd(t)和函数的最大幅值和v:
(2)
- 式的alpha;指数成为插入(ln v,ln Fd max)点的直线的斜率[图3(a)]。 基于该标准的校准过程给出了ED和PD装置的alpha;值约等于0.1(精确地为0.101和0.11)(Terenzi 1994)。为不同的alpha;值(1,0.2,0.1和0,其中最后一个值代表纯摩擦阻尼的极限条件)获得的选定Fd -u滞回曲线如图3(b)所示,这突出了这一参数对滞回曲线形状的影响。
图3.(a)试验得到的PD装置Fd max-v最大值和相关插补线;(b)不同alpha;值对应的Fd -u滞回曲线
通过最小化实验和分析计算的阻尼能量之间的差异来估计直接决定滞回环的幅值的c系数[后者通过关系式(1)计算]。 从ED和PD试验结果得到的平均值和标准偏差值[ED平均值= 14.7kN(s/mm)alpha;,标准差= 0.9kN(s/mm)alpha;;平均值= 55.2kN(s/mm)alpha;,标准偏差= 4.047kN(s/mm)alpha;]表明,该系数在速度和频率方面具有显着的稳定性。 在图4中可以观察到所提出的模型在匹配实验性能的全局特征方面的良好性能,其中从PD装置上进行的一个测试得到的响应循环叠加在分析的装置上。
关于ED装置的弹性性能,提出了如下抛物线和线性关系:
(3)
(4)
其中a,b和d 是三个常数,k 是弹性刚度。尽管抛物线函数更精确地再现了测试周期的形状(图5),但线性函数产生了可比较的能量平衡(Terenzi 1994; Chiarugi等人1995)。 因此,为了与本研究的一般线一致,且由于其参数的物理解释更简单,在下面的数值计算中将采用关系式(4)。
图4.PD装置:试验(——)和分析(- - - - -) 响应曲线(参考一个选定的试验所得)
图5.ED装置:试验(——)和分析(- - - - -) 响应曲线[(a),(b)是从线性或抛物线弹性关系中获得的解]
FrVD-SDOF体系的动态响应分析
自由和强迫振动响应的研究
结合关系式(1)和(4),受到一个随时间变化的力p(t)的FrVD-SDOF体系的运动方程变为
(5)
其中m 为体系的质量,是体系加速度时间历程。显然,在地震作用的情况下,p(t)可以写成,其中是地面加速度时间历程。
由于表征FrVD系统的特殊类型的阻尼函数,最通用的求解策略由(5)的直接数值积分表示。通过专门研究Argyris和Mlejnek(1991)提出的关于Newmark隐式法的一般程序,明确地建立了迭代求解算法(Terenzi 1994)。假设第k步迭代i的最多迭代次数为n,时间步是Delta;t,第(k 1)步可得位移,速度和加速度值如下:
(6a)
(6b)
(6c)
i=1,n (6d)
(6e)
(6f)
(6g)
其中和分别代表和项的第一个迭代值。 对于每个步骤,当满足条件(6g)时迭代循环即终止(在该分析中取迭代误差允许值ε= 0.001)。 这种积分方法可以很容易地编程,并且正如Argyris和Mlejnek(1991)对各种阻尼或机械非线性情况所证明的那样——并且进一步检查了分数粘滞阻尼的特殊情况(Terenzi 1994)——收敛非常迅速。
通过比较通过积分(5)得到的位移时间历程与具有线性粘滞阻尼或摩擦阻尼的SDOF元件所提供的位移时间历程,可以看出由非线性函数(1)引起的主要影响对于振荡器动态响应的影响。参考自由振动条件——例如悬臂梁——当梁受到阻尼并且其尖端通过线性粘滞阻尼器连接到地面时(所施加的力的大小与其瞬时速度成正比,方向相反),响应会及时消失,低阻尼器慢速消失,高阻尼器快速消失。衰减振荡的包络线是形式的指数曲线,其中delta;代表所谓的“对数衰减”,与第n与(n N)个周期振幅的比率有关,即
(7)
其中Un和Un N分别是第n和第(n N)个周期振幅。在这种情况下,delta;是阻尼量的量度。 当阻尼器由干摩擦组成时-其特征在于恒定的阻尼力,其在每个半周期改变符号以便在每个瞬间与速度方向相反,其衰减振荡的包络线是线性的。与前一个不同,在这种情况下,delta;不能被假定为阻尼的量度,因为其值不是唯一定义的。
分数粘滞阻尼代表线性粘滞阻尼和摩擦阻尼的极限情况之间的中间条件。这由(1)证明,其中阻尼力表示为速度符号的函数(类似于摩擦模型)和速度的幂[虽然不同于(1),即,对应于LVD体系的值]。如前一节所述,摩擦效应体现在与FrVD元件相关的滞回环的方形中。此外,如图6所示,叠画了分数粘性阻尼体系的自由振动响应与能量上等效的(即能够在相同激励下耗散相同量的能量)LVD体系的自由振动响应,FrVD振荡器的衰减位移包络线近似呈线性。另一方面,该系统对谐波变化激励的强迫振动响应更好地突出了与LVD模型显著的相似性。为了更好地研究这最后一个方面,可以通过开发表征LVD-SDOF元件的经典动态分析的相同步骤来讨论FrVD响应,其主要概念在下面简要回顾。
图6.FrVD和LVD体系的自由振动响应
当在时间t=0施加振荡力时,响应累积直到达到动态平衡,除了在没有阻尼的共振条件的特殊情况下,系统受到不断增加的振荡幅度。在实践中,总是存在一些阻尼,使系统在更高或更低的振幅下达到平衡,这取决于阻尼力的大小。
图7.受到正弦波作用的FrVD和LVD系统的位移时间历程(a)beta; = 0.5;(b)1; (c)2
FrVD-SDOF体系的时域响应的主要特征与线性粘滞振荡器体系没有实质性的不同,这代表了当受到频率低于,等于或大于这些系统频率的正弦波作用时具有相同质量和刚度的LVD和FrVD系统的响应的初步分析的主要结果。在每个数值试验中,FrVD振荡器被赋予了一个c值,以保证与线性粘滞体系具有相同耗散能量。如图7所示——其中位移时间历程和滞回环是通过对两个体系应用频率等于0.2 Hz[beta;= 0.5对应的输入动作,图7.(a)],0.4 Hz [beta;=1,图7.(b


