
英语原文共 7 页
采用Golay编码的时域反射计
改进合成布里渊光学器件的性能
Kenrsquo;ichi Nishiguchi
大阪大学大学工业合作办公室
开放实验室F-172,ISIR,8-1,Mihogaoka,茨城,大阪567-0047,日本
摘要
布里渊光时域研究进展-fletometry(BOTDR)技术使高分辨率分布式应变光纤传感和温度。然而,高空间分辨率botdr,例如合成botdr(s- BOTDR),具有一个弱点:频谱的信噪比是低于传统机器人。为了克服这个弱点,我们建议使用Golay代码序列。编码的S- BOTDR规格-Trum平均同意S-Boddr的观点;因此S- BOTDR的高空间分辨率特点是-服务。我们发现光谱的信噪比增加了重复次数可以减少一个编码的s-BOTDR,尽管存在所增加的码元长度不能超过一定限度。
1 介绍
布里渊光时域反射仪(BOTDR)是一种应变和分布式传感方法基于特性的光纤温度其中布里渊频谱按比例变化对应变和温度[1]。 传统的BOTDR将单脉冲注入光纤和通过外差来获得布里渊频谱布里渊背向散射光。 不幸的是,它的空间分辨率一直限制在1米[2]不适合许多应用。 为了克服这一点空间分辨率限制,双脉冲BOTDR(DP-BOTDR)[3],合成BOTDR(S-BOTDR)[4],和相移脉冲BOTDR(PSP-BOTDR)[5]已被提出。 而不是单脉冲传统的BOTDR,DP-BOTDR使用两个短脉冲,以及S-BOTDR和PSP-BOTDR使用由短和长组成的复合脉冲脉冲。使用这些BOTDR,10厘米的空间分辨率是可能的。然而,BOTDR具有如此高的空间分辨率问题:Bril-的信噪比(SNR)前景的技术[6]。 对于传统的BOTDR,如Go-等编码技术编码和单工编码已经是虽然空间分辨率很高,但它可以提高信噪比[7,8]lution被限制在1米。 对于DP-BOTDR,脉冲已经提出了使用巴克码[9]的压缩。在本文中,我们通过Go-应用相位调制将互补序列[10]放在S-BOTDR和表明SNR在保持高水平的同时得到了改善空间分辨率。现如今,电传感器的发展已经非常成熟,以其结构简单、成本低、测量精度高等特点而备受青睐。但在强电磁干扰或易燃、易爆的特殊环境下,电传感器便受到很大的限制。相比电传感器,光纤传感器具有提取关键信息和传送信号的双重功能,彰显出独特的优越性:抗电磁干扰能力强、具有长距离和分布式传感的能力、具有复用和多参数传感的功能、大带宽、高灵敏度等特点。尤其是光纤传感技术中的分布式光纤传感技术,只将光纤作为传感介质,把测参量作为光纤长度的函数,可以连续、准确地测量出整条光纤上任一点的重要信息,解决了传统点式传感技术监测漏的的问题,现已成为各种大型基础设施无损监测的最为理想的技术之一。
分布式光纤传感技术主要是利用光纤中的三种散射效应:瑞利散射(Rayleighscattering)效应、拉曼散射(Raman scattering)效应和布里渊散射(Brillouin scattering)效应。其中,布里渊散射对温度和应变都具有敏感性,可以实现温度和应变
的测量,并具有长距离传感、精度高、高信噪比等优点,因此如何提高传感系统的性能指标,一直是光纤传感领域研究的热点。1972年,Ippen等人在由玻璃材料制成的光纤中首次观测到布里渊散射现象。而后,研究者们又将光纤中的布里渊散射现象与温度和应变的关系广泛地应用到光纤传西南交通大学硕士研究生学位论文感技术中。当系统采用的传感光纤不同时,即使光纤上的温度或者应变相同,其引起的布里渊频移也不一定相同,但是温度或应变与布里渊频移都会呈现出某种线性关系。根据这种线性关系,1989年Horiguchi等人创造性地提出了基于受激布里渊散射放大效应的BOTDA技术,并且在1.2km的光纤上实现了100m空间分辨率的分布式温度传感1993年,Bao等人提出了布里渊损耗型的 BOTDA技术,并在 32km 的光纤上实现了 5m 空间分辨率的分布式温度传感。同年,TKurashima等人提出了基于自发布里渊散射的 BOTDR技术。而国内对基于布里渊散射的光纤传感技术的研究开始较晚。1999年,陈伟民、黄民双等人从理论上分析并推导了光纤中的布里渊频移与温度和应变之间的关系。华北电力大学则主要侧重于实现温度和应变同时传感的研究。浙江大学将信号处理技术应用到了BOTDR系统中。自2002年以来,南京大学光通信工程研究中心的张旭苹等人在提高空间分辨率、解决交叉敏感问题等方面进行了大量深入的研究工作,并将扫频和斜边辅助测量技术结合,用于测量振动信息。电子科技大学饶云江等人在基于拉曼放大和脉冲编码技术的长距离、高精度的BOTDA 方面做了很多研究,将系统传感距离提升到157km
2 S-BOTDR
S-BOTDR的框图如图1所示,其中使用不同探测灯的四次测量被祛除了。
图1 S-BOTDR的原理框图
四个探测灯由短脉冲组成图2中的f1(t)和长脉冲f 2(t)具有以下特征不同阶段差异:
f (j) (t) = f 1 (t) rlambda; j f 2 (t), j = 1,2,3,4, (1)
其中r是短路和短路之间的振幅比长脉冲和lambda;j,j = 1,2,3,4是相位因子被选中以满足:
在下文中,lambda;1= 1,lambda;2= i,lambda;3= -1,lambda;4= -i过去满足(2)。将探测光f(j)(t)注入光纤中,并且布里渊背向散射的光线与外延相互作用参考光以产生外差信号X(j)(t)。
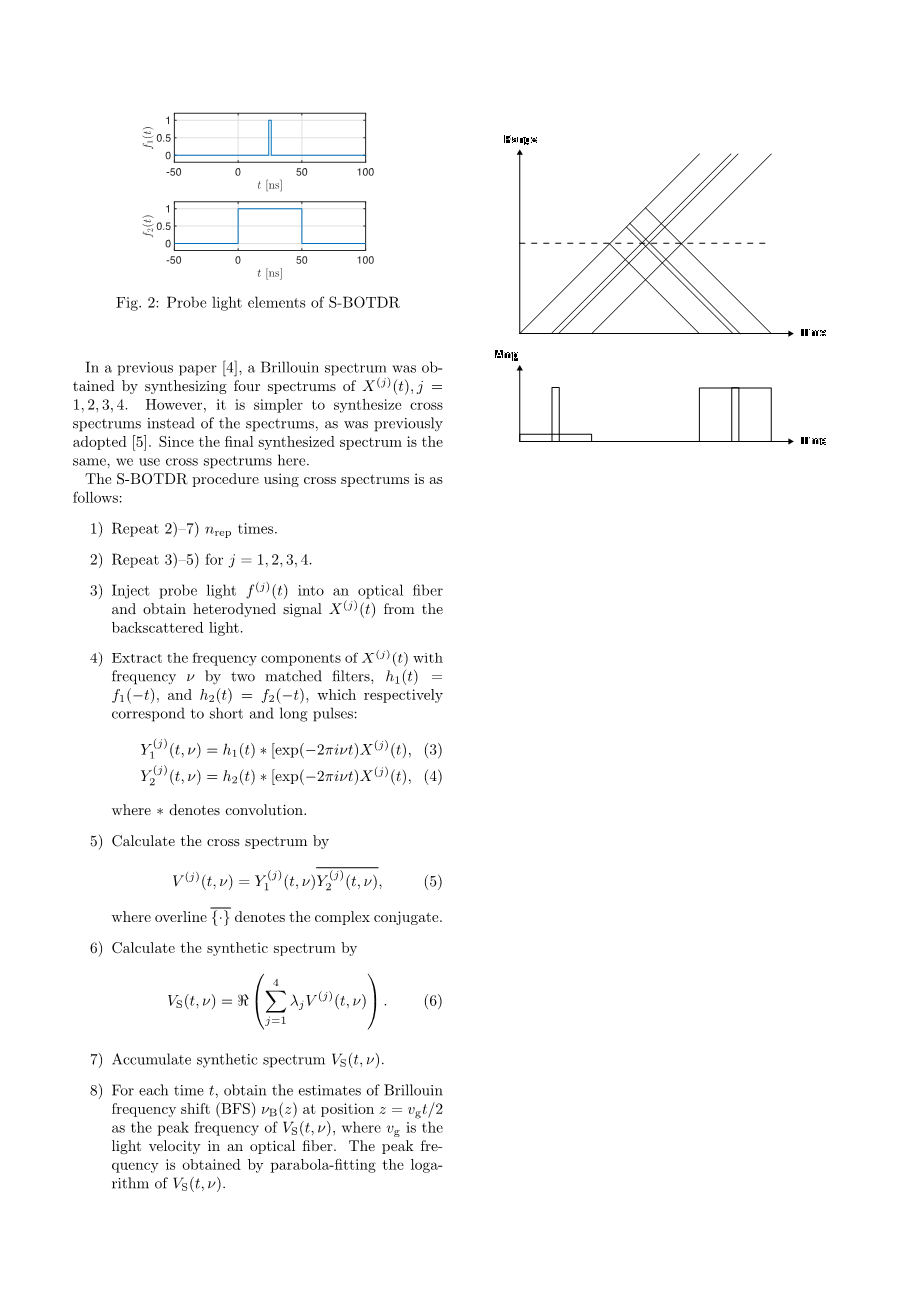
图2:S-BOTDR的探测光元件
在之前的论文[4]中,布里渊频谱是通过合成四个X(j)(t)光谱来获得,j =1,2,3,4。 但是,合成交叉更简单光谱而不是光谱,如前所述采纳[5]。 由于最终的合成光谱是同样,我们在这里使用交叉谱。使用交叉谱的S-BOTDR程序如下如下:
- 重复2)-7)n次代表。
- 对j = 1,2,3,4重复3)-5)。
- 将探测光f(j)(t)注入光纤并从中获得外差信号X(j)(t)反向散射光。
-
将探测光f(j)(t)注入光纤并从中获得外差信号X(j)(t)反向散射光。
用X(j)(t)提取频率分量频率nu;由两个匹配滤波器组成,h 1(t)=f 1(-t),h 2(t)= f 2(-t),它们反映短脉冲和长脉冲:
其中*表示卷积。
5)
通过计算合成光谱
累积合成光谱V S(t,nu;)。对于每个时间T,获得布里渊的估计值频率偏移(BFS)nu;B(z)在位置z = v g t / 2作为V S(t,nu;)的峰值频率,其中v g是光纤中的光速。最高频率通过抛物线拟合洛加获得V S(t,nu;)的公式。
对于任意固定的nu;,我们代表输出来自两个匹配的过滤器(3)和(4)如下:
Y(j)1=Y11 rlambda;jY21
Y(j)2=Y12 rlambda;jY22
其中Y kl,k,l = 1,2在右侧(RHS)表示提取的频率分量来自脉冲f k(·)的散射光由匹配滤波器h l(·)组成。这些对应于散射光的积分在图3中的不同颜色部分。真正的部分交叉谱Y 11 Y 22 [4]成为理想的布里渊如果短脉冲的脉冲宽度设置为,则为频谱所需的空间分辨率和长脉冲的空间分辨率被设定为比声子寿命足够长。探测光f(j)的交叉谱写为
期望可以通过累积来实现或平均通过获得的合成光谱许多重复测量。 但是,自高峰期以来由于其性质,光谱的功率很低高空间分辨率,光谱的相对波动 - 比传统的BOTDR更大重复测量的次数增加。
Fig. 4: Example of Golay codes, M = 16
3 基于Golay编码的S-BOTDR
为了提高S-BOTDR的SNR,我们使用了编码Golay代码的技术
一对代码序列,A k,B k,k = 0,1,...,M -1,如果是和的,则称为互补序列自相关满足。
其中delta;k,0冲激函数。Golay代码是二进制互补序列取值plusmn;1[10]可以通过以下附加生成方法:
下面是示例:
长度为16的Golay代码示例及其代码自相关如图4所示。我们对探针进行编码使用Golay码的S-BOTDR脉冲。其中delta;k,0是Kronecker delta。 Golay代码是二进制互补序列取值plusmn;1[10]可以通过以下附加生成方法:
在S-BOTDR中,四个复合脉冲组合在一起短脉冲和长脉冲用作探测灯。 对于每个复合脉冲,两个Golay码序列都是生成的; 总共产生8个序列八个探照灯。例如,以下序列用于aM = 4的Golay代码:
编码应用于短期或长期阶段脉冲。设d是复合脉冲的持续时间,并且让M为代码数量。 八探脉冲构造如下:
其中上标(A,j)和(B,j)分别代表代码序列(A,lambda;j)和(B,lambda;j)。 虽然在这种情况下,长脉冲被编码,短脉冲可以改为编码。 图5示出了编码的示例探测光和编码S-BOTDR的散射光M=4,其中短脉冲被编码。
图5:Golay的入射和散射光 -
图5 Golay互补码的入射光和S-BOTDR反射光
设X(A,j)(t),X(B,j)(t)j = 1,2,3,4为异 - 通过注入探针获得在时间t的信号灯f(A,j)(·),f(B,j)(·),j = 1,2,3,4。 编码S-具有信号处理的BOTDR程序如下:
1)重复2)-8)n次代表。
2)对j = 1,2,3,4重复3)-5)。
3)将探测光f(A,j)(t)注入光纤并从中获得外差信号X(A,j)(t)反向散射光。
4)提取X(A,j)(t)的频率分量频率nu;由两个匹配滤波器组成,h 1(t)=f 1(-t)和h 2(t)= f 2(-t),分别为
通过计算交叉谱:
获得V.(t,nu;),这是合成光谱关于B,通过与2)-6)相同的程序为一个。
累积合成光谱,解调反射光谱:
采取真实的部分或抽象的价值产生布里渊频谱。
对于每个时间t,估计nu;B(z),即BFS在位置z = v g t / 2处,作为峰值频率V S(t,nu;)。 峰值频率通过抛物线拟合V S(t,nu;)的对数。
4 Golay编码的性能分析S-BOTDR
对于任意固定的nu;,我们代表(15)和(16),两个匹配过滤器的输出,如下所示:Golay编码的性能分析S-BOTDR:
图6:复合材料之间距离的条件编码S-BOTDR的脉冲
将(17),(20)及(21)代入(18)并取代─按照预期,不受欢迎的条款被消除,如以前做过(10),屈服。
如果我们将(22)和(23)代入(24),它包括总结。 对于通过相关性解码,必须将总和减少到一个总和。因此,双重求和中的交叉项必须消失:
必须成立。这相当于两个条件区域,Y 11(t - md,nu;)和Y 22(t - (m 1)d,nu;)。
d ge; D1 D2 .
我们假设这个条件得到满足。有如下关系:
类似地,关于B 序列的合成光谱变成了
将(27)和(28)代入(19)在式(11)成立的情况下,我们有:
我们比较(10)S-BOTDR和频谱的期望变为2M倍而不是S-BOTDR。
由于布里渊的强度反向散射光是随机变量,布里渊频谱也是 - 是一个随机变量,它的前后波动。 导致这种波动的因素是信号波动和接收机噪声都是这是独立的因素。 设P峰值为expec-光谱峰值,sigma;2噪音和sigma;2sig是导致峰值功率波动的变化通过一个测量的噪声和信号波动 - 分别是。 我们定义了信噪比(SNR)用于一次测量。
对于n次重复测量,由于P峰值,sigma;2信号和sigma;2噪声都变大了n倍,表现出SNR如:
对于具有代码长度的编码布里渊频谱M,而P峰值和sigma;2噪声变大M倍,sigma;2SIG比非编码布里渊大2倍光谱,因为每个散射光包含M 脉冲信号来自不同点(图5)和M散灯在解码过程中相关。 因此,代码长度为M的编码S-BOTDR的SNR
比较。
这意味着SNR增加有一个限制。估计误差与估计误差之间的关系来自布里渊频谱的BFS和SNR是由[11]给出。
其中C是由因子决定的常数
SNR除外。 虽然是RHS的分母
是radic;SNR[11]因为使用了电气信噪比,所以上述等式适用于此中使用的光学SNR
纸。在图7中,绘制了BFS估计误差通过代入(32)得到的编码S-BOTDR(34)。 由于编码的S-BOTDR的SNR具有当M变大时,BFS估计误差也有一个下限,由曲线表示在图7中标记为M =infin;。
图7:理论BFS估计误差
5 通过模拟评估
我们进行了数值模拟来验证编码S-BOTDR并将其与非编码进行比较S-BOTDR。 假定的BFS在图8中给出。
图8:模拟条件:垂直轴代表固定距光纤输入端的距离和横轴,假设的BFS。
对于短脉冲,脉冲宽度为D 1 = 1 ns对于长脉冲,D 2 = 50 ns。 振幅比为r= 0.08。 短脉冲位于中心长脉冲。 探头灯的输入功率为20dBm的。 这些参数由S-BOTDR共享和编码的S-BOTDR。
显示了S-BOTDR的BFS估计结果在图9中,重复测量的次数是:
改为2 12,2 14和2 16。虽然没有5厘米的间自脉冲宽度以来,在所有情况下均检测到vals短脉冲为1 ns,相当于10 cm的温度 - 分辨率,其他间隔等于或大于10全部检测到厘米,包括边缘。估计重复精度随着重复次数的增加


